
【题目】在Rt△AEB中,∠AEB=90°,以斜边AB为边向Rt△AEB形外作正方形ABCD,若正方形ABCD的对角线交于点O(如图1).
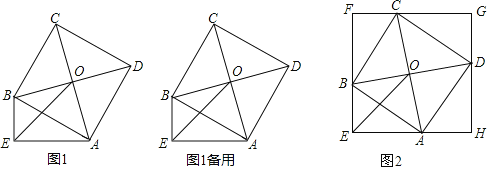
(1)求证:EO平分∠AEB;
(2)猜想线段OE与EB、EA之间的数量关系为 (直接写出结果,不要写出证明过程);
(3)过点C作CF⊥EB于F,过点D作DH⊥EA于H,CF和DH的反向延长线交于点G(如图2),求证:四边形EFGH为正方形.
【答案】(1)求证见解析;(2)![]() OE=EB+EA;(3)见解析.
OE=EB+EA;(3)见解析.
【解析】
(1)延长EA至点F,使AF=BE,连接OF,由SAS证得△OBE≌△OAF,得出OE=OF,∠BEO=∠AFO,由等腰三角形的性质与等量代换即可得出结论;
(2)判断出△EOF是等腰直角三角形,根据勾股定理即可得出结论;
(3)先根据ASA证得△ABE≌△ADH,△ABE≌△BCF,△ADH≌△DCG,△DCG≌△CBF,得出FG=EF=EH=HG,再由∠F=∠H=∠AEB=90°,由此可得出结论.
(1)证明:延长EA至点F,使AF=BE,连接OF,如图所示:
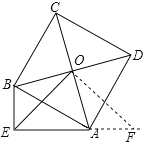
∵四边形ABCD是正方形,
∴∠BOA=90°,OB=OA,
∵∠AEB=90°,
∴∠OBE+∠OAE=360°﹣90°﹣90°=180°,
∵∠OAE+∠OAF=180°,
∴∠OBE=∠OAE,在△OBE与△OAF中,
 ,
,
∴△OBE≌△OAF(SAS),
∴OE=OF,∠BEO=∠AFO,
∴∠AEO=∠AFO,
∴∠BEO=∠AEO,
∴EO平分∠AEB;
(2)解:![]() OE=EB+EA,理由如下:
OE=EB+EA,理由如下:
由(1)得:△OBE≌△OAF,
∴OE=OF,∠BOE=∠AOF,
∵∠BOE+∠AOE=90°,
∴∠AOF+∠AOE=90°,
∴∠EOF=90°,
∴△EOF是等腰直角三角形,
∴2OE2=EF2,
∵EF=EA+AF=EA+EB,
∴2OE2=(EB+EA)2,
∴![]() OE=EB+EA,
OE=EB+EA,
故答案为:![]() OE=EB+EA;
OE=EB+EA;
(3)证明:∵CF⊥EB,DH⊥EA,
∴∠F=∠H=∠AEB=90°,
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∴∠EAB+∠DAH=90°,∠EAB+∠ABE=90°,∠ADH+∠DAH=90°,
∴∠EAB=∠HDA,∠ABE=∠DAH.
在△ABE与△ADH中,
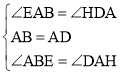 ,
,
∴△ABE≌△ADH(ASA),
∴BE=AH,AE=DH,
同理可得:△ABE≌△BCF,△ADH≌△DCG,△DCG≌△CBF,
∴BE=CF,AE=BF,AH=DG,DH=CG,DG=CF,CG=BF,
∴CG+FC=BF+BE=AE+AH=DH+DG,
∴FG=EF=EH=HG,
∵∠F=∠H=∠AEB=90°,
∴四边形EFGH为正方形.


科目:初中数学 来源: 题型:
【题目】阅读对人成长的影响是很大的,某中学共1500名学生.为了了解学生课外阅读的情况,就“你最喜欢的图书类别”(只选一项)随机调查了部分学生,并将调查结果统计后绘成如下统计表和统计图(如图).请你根据统计图表提供的信息解答下列问题:
(1)这次随机调查了 名学生;
(2)把统计表和条形统计图补充完整;
(3)随机调查一名学生,估计恰好是喜欢其他类图书的概率是 ;
(4)此学校想为校图书馆增加书籍,请根据调查结果,为学校选择一种学生最喜欢的书籍充实校图书馆,并说明理由;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋中,红球、黑球、白球共有若干个,除颜色外,形状、大小、质地等完全相同,小新从布袋中随机摸出一球,记下颜色后放回布袋中,摇匀后再随机摸出一球,记下颜色, ![]() 如此大量摸球实验后,小新发现其中摸出红球的频率稳定于
如此大量摸球实验后,小新发现其中摸出红球的频率稳定于![]() ,摸出黑球的频率稳定于
,摸出黑球的频率稳定于![]() ,对此实验,他总结出下列结论:
,对此实验,他总结出下列结论: ![]() 若进行大量摸球实验,摸出白球的频率稳定于
若进行大量摸球实验,摸出白球的频率稳定于![]() 若从布袋中任意摸出一个球,该球是黑球的概率最大;
若从布袋中任意摸出一个球,该球是黑球的概率最大; ![]() 若再摸球100次,必有20次摸出的是红球
若再摸球100次,必有20次摸出的是红球![]() 其中说法正确的是
其中说法正确的是![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】均匀的正四面体的各面依次标有![]() 四个数字
四个数字![]() 小明做了60次投掷试验,结果统计如下:
小明做了60次投掷试验,结果统计如下:
朝下数字 | 1 | 2 | 3 | 4 |
出现的次数 | 16 | 20 | 14 | 10 |
![]() 计算上述试验中“4朝下”的频率是多少?
计算上述试验中“4朝下”的频率是多少?
![]() “根据试验结果,投掷一次正四面体,出现2朝下的概率是
“根据试验结果,投掷一次正四面体,出现2朝下的概率是![]() ”的说法正确吗?为什么?
”的说法正确吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,矩形 ABCO 的边 OA 在 x 轴上,边 OC 在 y 轴上,点 B 的坐标为(3,4),直线 CD 分别交 OB、AB 于点 D、E,若 BD=BE,则点 D 的坐标为______.
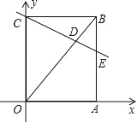
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正五边形ABCDE中,对角线![]() 与EB分别相交于点
与EB分别相交于点![]() 下列结论错误的是
下列结论错误的是![]()
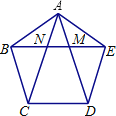
A. 四边形EDCN是菱形
B. 四边形MNCD是等腰梯形
C. ![]() 与
与![]() 相似
相似
D. ![]() 与
与![]() 全等
全等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, ⊙O 的半径是2,直线l与⊙O 相交于A、B 两点,M、N 是⊙O 上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB 面积的最大值是 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com