
【题目】学习完正多边形和圆后,在师生共同小结与归纳时,下面有几位同学谈了自己的想法.

针对以上三位同学的意见,谈谈自己的想法.
【答案】矩形不一定是正多边形,因为其各边不一定都相等,菱形不一定是正多边形,因为其各角不一定相等,正方形是正多边形;圆内接菱形是正方形,因为菱形各边相等,且各边所对的弧也相等,可推出其各内角也都相等;正多边形是轴对称图形,但不一定是中心对称图形.
【解析】试题分析:根据正多边形是各边都相等,各角都相等的多边形,圆内接四边形的对角互补,以及轴对称图形和中心对称图形的概念解答.
试题解析:胡思:各边都相等,各角都相等的角的四边形是正多边形,所以正方形是正多边形,矩形、菱形不是正多边形.
胡洋:因为圆内接四边形的对角互补,则圆内接菱形是正方形,故说法正确.
李军:所有的正多边形是轴对称图形,只有边数是偶数的正多边形才是中心对称图形.


科目:初中数学 来源: 题型:
【题目】在学校组织的以”垃圾分类 从我做起“的主题知识竞赛活动中,王老师随机抽取了班中参赛的6名学生成绩,若以80分为标准,超过这个分数用正数表示,不足的分数用负数表示,成绩记录如下:-3,+7,-12,+6 , -21 ,+14
(1) 最高分比最低分多多少分?这6名学生平均每人得多少分?
(2) 若规定:成绩高于80分的学生操行分每人加3分,成绩在60~80分的学生操行分每人加2分,成绩在60分以下的学生操行分每人扣1分,那么这6名学生共加操行分多少分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知□ABCD,延长AB到E使BE=AB,连接BD,ED,EC,若ED=AD.
(1)求证:四边形BECD是矩形;
(2)连接AC,若AD=4,CD= 2,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=1,BC=3.
(1)在图①中,P是BC上一点,EF垂直平分AP,分别交AD、BC边于点E、F,求证:四边形AFPE是菱形;
(2)在图②中利用直尺和圆规作出面积最大的菱形,使得菱形的四个顶点都在矩形ABCD的边上,并直接标出菱形的边长.(保留作图痕迹,不写作法)
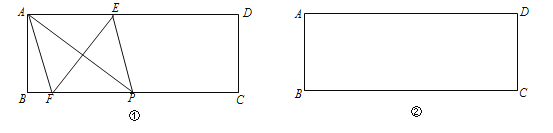
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周长相等的正三角形、正四边形、正六边形的面积S3、S4、S6间的大小关系是( )
A. S3>S4>S6 B. S6>S4>S3 C. S6>S3>S4 D. S4>S6>S3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形ABCD为正方形,已知点A(-6,0),D(-7,3),点B、C在第二象限内.
(1)点B的坐标 ;
(2)将正方形ABCD以每秒1个单位的速度沿x轴向右平移t秒,若存在某一时刻t,使在第一象限内点B、D两点的对应点B′、D′正好落在某反比例函数的图象上,请求出此时t的值以及这个反比例函数的解析式;
(3)在(2)的情况下,问是否存在x轴上的点P和反比例函数图象上的点Q,使得以P、Q、B′、D′四个点为顶点的四边形是平行四边形?若存在,请求出符合题意的点P、Q的坐标;若不存在,请说明理由.

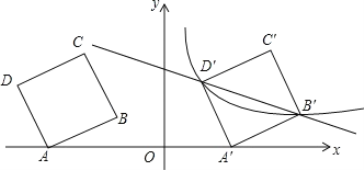
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在有些情况下,不需要计算出结果也能把绝对值符号去掉.
例如: |6+7|=6+7 ; |6-7|=7-6 ; |7-6|=7-6 ; |-6-7|=6+7.
(1)根据上面的规律,把下列各式写成去掉绝对值符号的形式:
①|7-21|=_____;②![]() =_____;③
=_____;③![]() =_____;④│a-b│=____(a<b);
=_____;④│a-b│=____(a<b);
(2)用合理的方法计算:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△AEB中,∠AEB=90°,以斜边AB为边向Rt△AEB形外作正方形ABCD,若正方形ABCD的对角线交于点O(如图1).
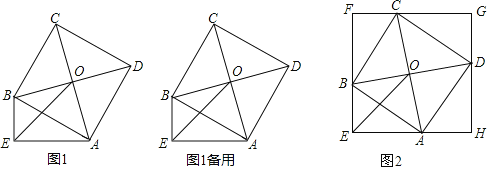
(1)求证:EO平分∠AEB;
(2)猜想线段OE与EB、EA之间的数量关系为 (直接写出结果,不要写出证明过程);
(3)过点C作CF⊥EB于F,过点D作DH⊥EA于H,CF和DH的反向延长线交于点G(如图2),求证:四边形EFGH为正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某摩托车厂本周计划每日生产450辆摩托车,由于工人实行轮休, 每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表: [增加的辆数为正数,减少的辆数为负数]
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 | -5 | +7 | -3 | +4 | +10 | -9 | -25 |
(1)本周星期六生产多少辆摩托车?
(2)本周总产量与计划产量相比,是增加了还是减少了?为什么?
(3)产量最多的那天比产量最少的那天多生产多少辆?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com