练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．下列多边形中，能够铺满地面的是（　　）
    A．正方形B．正五边形C．正七边形D．正八边形

    分析 分别求出各个正多边形的每个内角的度数，结合镶嵌的条件即可作出判断．

    解答 解：A、正方形的每个内角是90°，4个能密铺，符合题意；
    B、正五边形每个内角是180°-360°÷5=108°，不能整除360°，不能密铺，不符合题意；
    C、正七边形每个内角是180°-360°÷7=$\frac{900}{7}$，不能整除360°，不能密铺，不符合题意；
    D、正八边形每个内角是180°-360°÷8=135°，不能整除360°，不能密铺，不符合题意．
    故选：A．

    点评 本题考查了一种多边形的镶嵌问题，考查的知识点是：一种正多边形的镶嵌应符合一个内角度数能整除360°．任意多边形能进行镶嵌，说明它的内角和应能整除360°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

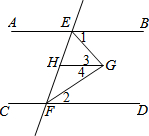    17．完成下面的证明：
    已知：如图，AB∥CD∥GH，EG平分∠BEF，FG平分∠EFD，求证：∠EGF=90°．
    证明：∵HG∥AB，HG∥CD （已知）；
    ∴∠1=∠3
    ∴∠2=∠4两直线平行，内错角相等．
    ∵AB∥CD（已知）；
    ∴∠BEF+∠EFD=180°两直线平行，同旁内角互补．
    又∵EG平分∠BEF，FG平分∠EFD（已知）
    ∴∠1=$\frac{1}{2}$∠角平分线的定义
    ∠2=$\frac{1}{2}$∠EFD．
    ∴∠1+∠2=$\frac{1}{2}$（∠BEF+∠EFD）．
    ∴∠1+∠2=90°；
    ∴∠3+∠4=90°，即∠EGF=90°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．已知$\sqrt{24a}$是整数，a是正整数，a的最小值是（　　）
    A．0B．3C．6D．24

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．如图所示的四棱台，它的俯视图是下面所示的图形的（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

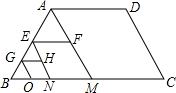    2．如图，四边形ABCD是等腰梯形，BC=2AD=4，过A作AM∥DC，得到第1个三角形，其平行于BC的中位线EF=1；过E作EN∥DC，得到第2个三角形，其平行于BC的中位线GH=$\frac{1}{2}$；过G作GO∥DC，得到第3个三角形，…．按此规律作出第n个三角形，则其平行于BC的中位线长等于$\frac{1}{{2}^{n-1}}$．（用正整数n表示）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．解不等式$\frac{2x+1}{3}$-$\frac{x-1}{6}$≥2，并把解集表示在数轴上．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

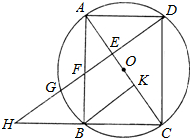    19．如图，已知：矩形ABCD，以对角线AC的中点O为圆心，OA的长为半径作⊙O，⊙O经过B、D两点，过点B作BK⊥AC，垂足为点K，过点D作DH∥KB，DH分别与AC、AB、⊙O及CB的延长线相交于点E、F、G、H．
    （1）求证：AE=CK；
    （2）若F是EG的中点，且DE=6，求⊙O的半径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

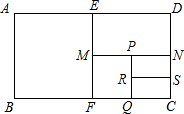    16．如图，在矩形ABCD中，AB=a，将矩形ABCD沿EF对折后，得ABFE和矩形EFCD，然后再把其中的一个矩形EFCD沿MN对折，得矩形MNCF和矩形MNDE，…，依此类推，得矩形PRSN和RQCS，并且所有矩形都相似，则RS等于（　　）
    A．$\frac{\sqrt{2}}{8}$aB．$\frac{\sqrt{2}}{4}$aC．$\frac{\sqrt{2}}{2}$aD．$\frac{1}{4}$a

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．龙东东同学家买了一辆轿车，他连续10天记录了他家轿车每天行驶的路程，以40KM为标准，超过或不足的分别用正数、负数表示，得到的数据分别如下（单位：KM）：+2，-4，+5，-3，+2，+3，+1，-2，+4，-8
    （1）请你运用所学知识估计龙东东家一个月（按30天算）轿车行驶的路程；
    （2）若已知该轿车每行驶100KM耗用汽油7升，且汽车的价格为每升7.20元，请你根据第（1）题估计龙东东家轿车一年（按12个月计算）的汽油费用．

    查看答案和解析>>

    同步练习册答案