
分析 (1)设乙盒中红球的个数为x个,根据概率公式得到$\frac{x}{x+2}$=$\frac{3}{5}$,然后解分式方程即可;
(2)先利用列表展示所有10种等可能的结果,再找出两次摸到不同颜色的球的结果数,然后根据概率公式求解.
解答 解:(1)设乙盒中红球的个数为x个,
根据题意得$\frac{x}{x+2}$=$\frac{3}{5}$,解得x=3
经检验,x=3是方程的根.
答:乙盒中红球的个数为3;
(2)列表如下: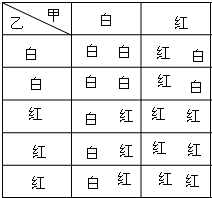
共有10种等可能的结果,两次摸到不同颜色的球的结果数为5,
所以两次摸到不同颜色的球的概率=$\frac{5}{10}$=$\frac{1}{2}$.
点评 本题考查了列表法或树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
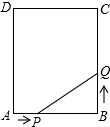 如图.矩形ABCD中,AB=6cm,BC=10cm,点P从A开始沿AB边向点B以1厘米/秒的速度移动,点Q从点B开始沿BC边向点C以2厘米/秒的速度移动,如果P、Q分别是从A、B同时出发,经过几秒,五边形APQCD的面积等于52平方厘米?
如图.矩形ABCD中,AB=6cm,BC=10cm,点P从A开始沿AB边向点B以1厘米/秒的速度移动,点Q从点B开始沿BC边向点C以2厘米/秒的速度移动,如果P、Q分别是从A、B同时出发,经过几秒,五边形APQCD的面积等于52平方厘米?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
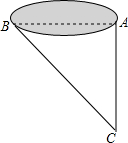 如图所示,某工程队修建高速公路,需打通一条东西走向的隧道AB,为了测得AB的长,工程队在A处正南方向800米的C处测得BC=1000米,则隧道AB的长为600米.
如图所示,某工程队修建高速公路,需打通一条东西走向的隧道AB,为了测得AB的长,工程队在A处正南方向800米的C处测得BC=1000米,则隧道AB的长为600米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com