
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 的中点,以
的中点,以![]() 为一边向外作等边三角形
为一边向外作等边三角形![]() ,连结
,连结![]() .
.
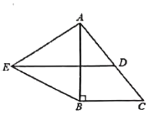
(1)证明: ![]() ;
;
(2)探索![]() 与
与![]() 满足怎样的数量关系时,四边形
满足怎样的数量关系时,四边形![]() 是平行四边形;
是平行四边形;
【答案】(1)见解析;(2)当![]() 或
或![]() 时,四边形
时,四边形![]() 是平行四边形,见解析.
是平行四边形,见解析.
【解析】
(1)连结BD,根据直角三角形的性质可得BD=![]() AC=AD,利用等边三角形的性质可得AE=BE,然后证明△ADE≌△BDE,进而可求出∠AED=∠BED=30°,
AC=AD,利用等边三角形的性质可得AE=BE,然后证明△ADE≌△BDE,进而可求出∠AED=∠BED=30°,
然后再证明∠BED+∠EBC=180°,从而可得结论;
(2)当AB=![]() AC或AC=2AB时,四边形DCBE是平行四边形,首先利用三角函数求出∠C=30°,然后证明DC∥BE,再有DE∥BC,可得四边形DCBE是平行四边形.
AC或AC=2AB时,四边形DCBE是平行四边形,首先利用三角函数求出∠C=30°,然后证明DC∥BE,再有DE∥BC,可得四边形DCBE是平行四边形.
解:(1)连结![]() .
.
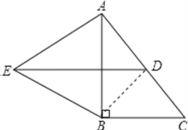
因为点![]() 为
为![]() 的斜边
的斜边![]() 的中点,
的中点,
所以![]() ,
,
![]() 是等边三角形,
是等边三角形,![]() ,
,
在![]() 与
与![]() 中,
中,
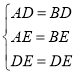 ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ;
;
(2)当![]() 或
或![]() 时,四边形
时,四边形![]() 是平行四边形.
是平行四边形.
理由:![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
又![]() ,∴四边形
,∴四边形![]() 是平行四边形.
是平行四边形.
故答案为:(1)见解析;(2)当![]() 或
或![]() 时,四边形
时,四边形![]() 是平行四边形,见解析.
是平行四边形,见解析.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】课题小组从某市2000名九年级男生中,随机抽取了1000名进行50米跑测试,并根据测试结果制成了如下的统计表.
等级 | 人数 | 百分比 |
优秀 | 200 | 20% |
良好 | 600 | 60% |
及格 | 150 | 15% |
不及格 | 50 |
|
(1)![]() 的值为______;
的值为______;
(2)请从表格中任意选取一列数据,绘制合理的统计图来表示;(绘制一种即可)
(3)估计这20000名九年级男生中50米跑达到良好和优秀等级的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县教育局今年体育测试中,从某校毕业班中抽取男,女学生各15人进行三项体育成绩复查测试.在这个问题中,下列叙述正确的是( )
A.该校所有毕业班学生是总体B.所抽取的30名学生是样本
C.样本的容量是15D.个体指的是毕业班每一个学生的体育测试成绩
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B,M两点的⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径.

(1)求证:AE与⊙O相切;
(2)当BC=4,cosC=![]() 时,求⊙O的半径.
时,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架,书中的算法体系至今仍在推动着计算机的发展和应用.《九章算术》中记载:今有户不知高、广,竿不知长、短.横之不出四尺,从之不出二尺,邪之适出.问户高、广、邪各几何?译文是:今有门不知其高、宽,有竿,不知其长、短,横放,竿比门宽长出![]() 尺;竖放,竿比门高长出
尺;竖放,竿比门高长出![]() 尺;斜放,竿与门对角线恰好相等.问门高、宽、对角线长分别是多少?若设门对角线长为
尺;斜放,竿与门对角线恰好相等.问门高、宽、对角线长分别是多少?若设门对角线长为![]() 尺,则可列方程为__________.
尺,则可列方程为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在解一元二次方程时,发现有这样一种解法:
如:解方程x(x+4)=6.
解:原方程可变形,得:[(x+2)﹣2][(x+2)+2]=6.
(x+2)2﹣22=6,
(x+2)2=6+22,
(x+2)2=10.
直接开平方并整理,得.x1=﹣2+![]() ,x2=﹣2﹣
,x2=﹣2﹣![]() .
.
我们称小明这种解法为“平均数法”.
(1)下面是小明用“平均数法”解方程(x+3)(x+7)=5时写的解题过程.
解:原方程可变形,得:[(x+a)﹣b][(x+a)+b]=5.
(x+a)2﹣b2=5,
(x+a)2=5+b2.
直接开平方并整理,得.x1=c,x2=d.
上述过程中的a、b、c、d表示的数分别为 , , , .
(2)请用“平均数法”解方程:(x﹣5)(x+3)=6.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平面直角坐标系![]() 中,正比例函数
中,正比例函数![]() 与一次函数
与一次函数![]() 的图象相交于点
的图象相交于点![]() ,过点
,过点![]() 作
作![]() 轴的垂线,分别交正比例函数的图像于点B,交一次函数的图象于点C,连接OC.
轴的垂线,分别交正比例函数的图像于点B,交一次函数的图象于点C,连接OC.
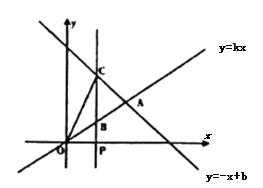
(1)求这两个函数解析式.
(2)求![]() 的面积.
的面积.
(3)在坐标轴上存在点![]() ,使
,使![]() 是以
是以![]() 为腰的等腰三角形,请直接写出
为腰的等腰三角形,请直接写出![]() 点的坐标。
点的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,求巡逻船从出发到成功拦截捕鱼船所用的时间.
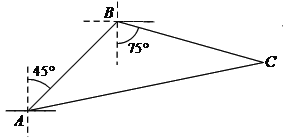
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com