

���� ��1����������y=-x2+bx+9-b2��bΪ��������������ԭ��O���ɵó�����b��һԪ���η��̣��ⷽ�̿ɵó�b=��3�����������ߵĶ����ڵ�һ���ޣ���ȷ��b��ֵΪ3���ɴ˿ɵó������ߵĽ���ʽ����x=1���������߽���ʽ���ɵó���B�����ꣻ
��2�����ݵ�B������ɵó�ֱ��OB�Ľ���ʽ�����P������Ϊ��m��0�������E������Ϊ��m��2m�����ɵ���ֱ�������ε����ʿɵó���C������Ϊ��3m��2m����������������߽���ʽ�����m��ֵ���ɴ˿ɵó�OP�ij���
��3�����F������Ϊ��n��-n2+3n����0��n��$\frac{3}{2}$������G������Ϊ��3-n��-n2+3n����Q�������Ϊ��n��0��������F��G��Q������꼴���ú�n�Ĵ���ʽ��ʾ������FQNG�ij��Ϳ�����Ͼ��ε��ܳ���ʽ�ɵó��ܳ�C����n�ĺ�����ϵʽ�����ö��κ��������ʼ��ɽ����ֵ���⣮
��� �⣺��1����������y=-x2+bx+9-b2��bΪ��������������ԭ��O��
��9-b2=0����ã�b=-3����b=3��
�������ߵĶԳ���Ϊx=-$\frac{b}{2����-1��}$=$\frac{b}{2}$������M�ڵ�һ���ޣ�
��b=3��
�������ߵĽ���ʽΪy=-x2+3x��
�ߵ�B��1��n���������������ϣ�
��n=-1+3=2��
���B��������1��2����
��2����ֱ��OB�Ľ���ʽΪy=kx��
�ߵ�B������Ϊ��1��2����
����2=k��
��ֱ��OB�Ľ���ʽΪy=2x��
���P��������m��0�������E��������m��2m����
��������PCDΪ����ֱ�������Σ�
��PE=EC=2m��
���C��������3m��2m����
�ߵ�C��������y=-x2+3x�ϣ�
����2m=-9m2+9m��
��ã�m=0����ȥ������m=$\frac{7}{9}$��
����P��������$\frac{7}{9}$��0����
��OP�ij���Ϊ$\frac{7}{9}$��
��3��������y=-x2+3x�ĶԳ���Ϊx=-$\frac{3}{2����-1��}$=$\frac{3}{2}$��
���F��������n��-n2+3n����0��n��$\frac{3}{2}$������G��������3-n��-n2+3n����Q���������n��0����
��FQ=-n2+3n��FG=3-n-n��
����FQNG���ܳ�C=2��FQ+FG��=2��-n2+3n+3-2n��=-2n2+2n+6=-2$��n-\frac{1}{2}��^{2}$+$\frac{13}{2}$��
�൱n=$\frac{1}{2}$ʱ������FQNG���ܳ�ȡ���ֵ$\frac{13}{2}$����ʱ��F������Ϊ��$\frac{1}{2}$��$\frac{5}{4}$����
���� ���⿼���˶��κ�����Ӧ�á�����ϵ������������ʽ������ֱ�������ε������Լ����ε��ܳ���ʽ������Ĺؼ��ǣ���1�����b��ֵ����2���ú�m�Ĵ���ʽ��ʾ����C�����ꣻ��3���ҳ��ܳ�C����n�ĺ�����ϵʽ�����������е��⣬�ѶȲ������������Ŀʱ�����������꣬��������ϵ�ҳ����ڵ�������е�δ֪���ķ��̣��ⷽ����ȷ����������ǹؼ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
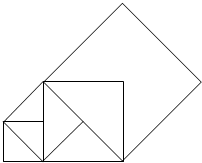 ��ͼ���Ȼ�һ���߳�Ϊ1�������Σ�����Խ���Ϊ���ڶ��������Σ����Եڶ��������εĶԽ���Ϊ�������������Σ�������˷�����ȥ����ô��n�������εĶԽ��߳�Ϊ��$\sqrt{2}$��n��
��ͼ���Ȼ�һ���߳�Ϊ1�������Σ�����Խ���Ϊ���ڶ��������Σ����Եڶ��������εĶԽ���Ϊ�������������Σ�������˷�����ȥ����ô��n�������εĶԽ��߳�Ϊ��$\sqrt{2}$��n���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
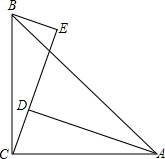 ��ͼ����ACB=90�㣬BC=AC��AD��CE��BE��CE������ֱ�ΪD��E��AD=2.5cm��BE=0.8cm����DE�ij���
��ͼ����ACB=90�㣬BC=AC��AD��CE��BE��CE������ֱ�ΪD��E��AD=2.5cm��BE=0.8cm����DE�ij����鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com