
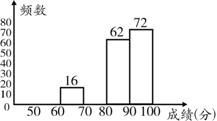
某市八年级有3000名学生参加“爱我中华知识竞赛”活动.为了了解本次知识竞赛的成绩分布情况,从中随机抽取了200名学生的得分进行统计.
请你根据不完整的表格,解答下列问题:
(1)补全频数分布表;
(2)补全频数分布直方图;
(3)若将得分转化为等级,规定50≤x<60评为“D”,60≤x<70评为“C”,70≤x<90评为“B”,90≤x<100评为“A”.估计这3000名学生中,有多少学生得分等级为A?
| 成绩 x 分 | 频数 | 频率 |
| 50≤x<60 | 10 |
|
| 60≤ x <70 | 16 | 0.08 |
| 70≤ x <80 |
| 0.2 |
| 80≤ x <90 | 62 | 0.31 |
| 90≤ x <100 | 72 | 0.36 |
 |
科目:初中数学 来源: 题型:
四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这 个四边形是平行四边形的是 ( )
个四边形是平行四边形的是 ( )
A.AB//DC,AD//BC B.AB//DC,AD=BC
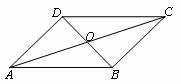 C.AO=CO,BO=DO D
C.AO=CO,BO=DO D .AB=DC,AD=BC
.AB=DC,AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
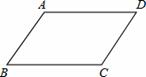
如图,已知四边形ABCD是平行四边形,若点E、F分别在边BC、AD上,连接AE、CF,请再从下列三个备选条件中,选择添加一个恰当的条件.使四边形AECF是平行四边形,并予以证明,
备选条件:AE=CF,BE=DF,∠AEB=∠CFD,
我选择添加的条件是 .证明:
查看答案和解析>>
科目:初中数学 来源: 题型:
邻边不相等的平行四边形纸片,剪去一个菱形,余下一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又余下一个四边形,称为第二次操作;……依此类推,若第n次操作余下的四边形是菱形,则称原平行四边形为n阶准菱形.如图1,□ABCD中,若AB=1,BC=2,则□ABCD为1阶准菱形.
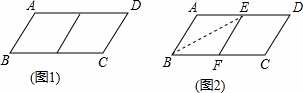 |
(1)判断与推理:
①邻边长分别为2和3的平行四边形是 阶准菱形;
②小明为了剪去一个菱形,进行如下操作:如图2,把□ABCD沿BE折叠(点E在AD上),使点A落在BC边上的点F,得到四边形ABFE.请证明四边形ABEF是菱形.
(2)操作、探究与计算:
①已知□ABCD是邻边长分别为1,a(a>1),且是3阶准菱形,请画出□ABCD及裁剪线的示意图,并在图形下方写出a的值;
②已知□ABCD的邻边长分别为a,b(a>b),满足a=6b+r,b=5r(r>0),则□ABCD是 阶准菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,如果AB∥CD,则角α、β、γ之间的关系式为( )
A.α+β+γ=360º B.α-β+γ=180º
C.α+β+γ=180º D.α+β-γ=180º
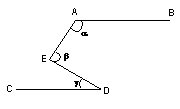
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,L1,L2分别表示一种白炽灯和一种节能灯的费用y(费用=灯的售价+电费,单位:元)与照明时间x(h)的函数图像,
(1)根据图像分别求出L1,L2的函数关系式.
 (
( 2)当照明时间为多少时,两种灯的费用相等?
2)当照明时间为多少时,两种灯的费用相等?
(3)假设两种灯的使用寿 命都是2000h,照明效果一样.小亮房间计划照明2500h,他买了一个白炽灯和一个节能灯,请你帮他设计最省钱的用灯方法(直接给出答案,不必写出解答过程).
命都是2000h,照明效果一样.小亮房间计划照明2500h,他买了一个白炽灯和一个节能灯,请你帮他设计最省钱的用灯方法(直接给出答案,不必写出解答过程).
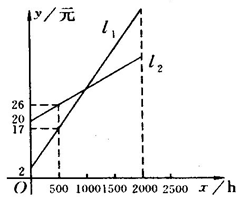
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知四边形ABCD中,R、P分别是BC、CD上的点,E、F分别是AP、RP的中点,当点P在CD上从C向D移动而点R不动时,那么下列结论成立的是( )
A.线段EF的长逐渐增大 B.线段EF的长逐渐减小
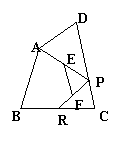 C.线段EF的长不变
C.线段EF的长不变  D.线段EF的长与点P的位置有关
D.线段EF的长与点P的位置有关
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com