Question

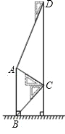
【题目】如图，将一张矩形纸片ABCD沿直线MN折叠，使点C落在点A处，点D落在点E处，直线MN交BC于点M，交AD于点N．

（1）求证：CM=CN；

（2）若△CMN的面积与△CDN的面积比为3：1，且CD=4，求线段MN的长．

Answer 1

【答案】（1）证明见解析；（2）．

【解析】

试题（1）由折叠的性质可得：∠ANM=∠CNM，由四边形ABCD是矩形，可得∠ANM=∠CMN，则可证得∠CMN=∠CNM，继而可得CM=CN．

（2）首先过点N作NH⊥BC于点H，由△CMN的面积与△CDN的面积比为3：1，易得MC=3ND=3HC，然后设DN=x，由勾股定理，可求得MN的长．

（1）由折叠的性质可得：∠ANM=∠CNM ．

∵ 四边形ABCD是矩形，

∴ AD∥BC ．

∴ ∠ANM=∠CMN ．

∴ ∠CMN=∠CNM ．

∴ CM=CN．

（2）如图，过点N作NH⊥BC于点H，则四边形NHCD是矩形．

∴HC=DN，NH=DC．

∵ △CMN的面积与△CDN的面积比为3：1，

∴ MC=3ND=3HC．

∴ MH=2HC．

设DN=x，则HC=x，MH=2x，

∴CM=3x=CN．

在Rt△CDN中，DC=2x=4，

∴．

∴HM=2．

在Rt△MNH中，MN=．