
【题目】观察如图图形,把一个三角形分别连接其三边中点,构成4个小三角形,挖去中间的一个小三角形(如图1),对剩下的三个小三角形再分别重复以上做法,……,据此解答下面的问题
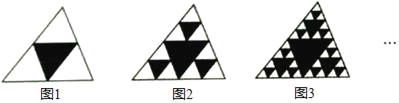
(1)填写下表:
图形 | 挖去三角形的个数 |
图形1 | 1 |
图形2 | 1+3 |
图形3 | 1+3+9 |
图形4 |
|
(2)根据这个规律,求图n中挖去三角形的个数wn;(用含n的代数式表示)
(3)若图n+1中挖去三角形的个数为wn+1,求wn+1﹣Wn
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图①,已知线段 AB=12cm,点 C 为 AB 上的一个动点,点 D,E 分别是 AC 和 BC的中点.
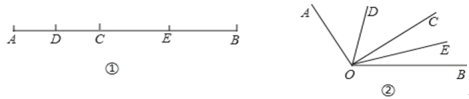
(1)若 AC=4cm,求 DE 的长.
(2)若 AC=acm(不超过 12cm),求 DE 的长.
(3)知识迁移:如图②,已知∠AOB=120°,过角的内部任意一点 C 画射线OC,若OD,OE 分别平分∠AOC 和∠BOC,求∠DOE 的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某片果园有果树80棵,现准备多种一些果树提高果园产量,但是如果多种树,那么树之间的距离和每棵树所受光照就会减少,单棵树的产量随之降低,若该果园每棵果树产果y千克,增种果树x棵,它们之间的函数关系如图所示.

(1)求y与x之间的函数解析式;
(2)在投入成本最低的情况下,增种果树多少棵时,果园可以收获果实6750千克?
(3)当增种果树多少棵时,果园的总产量w(千克)最大?最大产量是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若线段AB上有一点P,当PA=PB时,则称点P为线段AB的中点。
已知数轴上A,B两点对应数分别为a和b,![]() ,P为数轴上一动点,对应数为x.
,P为数轴上一动点,对应数为x.
(1)a=______,b=_______;
(2)若点P为线段AB的中点,则P点对应的数![]() 为______________.若B为线段AP的中点时则P点对应的数
为______________.若B为线段AP的中点时则P点对应的数![]() 为______________。
为______________。
(3)若点A、点B同时向左运动,它们的速度都为1个单位长度/秒,与此同时点P从-16处以2个单位长度/秒向右运动。
①设运动的时间为t秒,直接用含t的式子填空
AP=____________;BP=______________。
②经过多长时间后,点A、点B、点P三点中其中一点是另外两点的中点?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的弦,半径OA=2,OA和AB的长度是关于x的一元二次方程x2﹣4x+a=0的两个实数根.
(1)求弦AB的长度;
(2)计算S△AOB;
(3)⊙O上一动点P从A点出发,沿逆时针方向运动一周,当S△POA=S△AOB时,求P点所经过的弧长(不考虑点P与点B重合的情形).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣kx+k2+n=0有两个不相等的实数根x1、x2,且(2x1+x2)2﹣8(2x1+x2)+15=0.
(1)求证:n<0;
(2)试用k的代数式表示x1;
(3)当n=﹣3时,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB//CD,点C在点D的右侧,∠ABC,∠ADC的平分线交于点E(不与B,D点重合).![]() ,
,![]() .
.
(1)若点B在点A的左侧,求∠BED的度数(用含![]() 的代数式表示).
的代数式表示).
(2)将线段BC沿DC方向平移,当点B移动到点A右侧时,请画出图形并判断![]() 的度数是否改变.若改变,请求出
的度数是否改变.若改变,请求出![]() 的度数(用含
的度数(用含![]() 的代数式表示);若不变,请说明理由.
的代数式表示);若不变,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com