

分析 (1)首先根据角平分线的定义求得∠COF,然后求得∠BOC的度数,根据角平分线的定义求得∠EOC,然后根据∠EOF=∠COF+∠EOC求解;
(2)根据角平分线的定义可以得到∠COF=$\frac{1}{2}$∠AOC,∠EOC=$\frac{1}{2}$∠BOC,然后根据∠EOF=∠COF+∠EOC=$\frac{1}{2}$∠AOC+$\frac{1}{2}$∠BOC=$\frac{1}{2}$(∠AOC+∠BOC)即可得到;(3)根据∠EOB=$\frac{1}{3}$∠COB,可以得到,∠EOC=$\frac{2}{3}$∠COB,则∠EOF=∠EOC+∠COF=$\frac{2}{3}$∠BOC+$\frac{2}{3}$∠AOC=$\frac{2}{3}$∠AOB,从而求解.
解答 解:(1):(1)∵OF平分∠AOC,
∴∠COF=$\frac{1}{2}$∠AOC=$\frac{1}{2}$×30°=15°,
∵∠BOC=∠AOB-∠AOC=90°-30°=60°,OE平分∠BOC,
∴∠EOC=$\frac{1}{2}$∠BOC=30°,
∴∠EOF=∠COF+∠EOC=45°;
(2))∵OF平分∠AOC,
∴∠COF=$\frac{1}{2}$∠AOC,
同理,∠EOC=$\frac{1}{2}$∠BOC,
∴∠EOF=∠COF+∠EOC=$\frac{1}{2}$∠AOC+$\frac{1}{2}$∠BOC=$\frac{1}{2}$(∠AOC+∠BOC)=$\frac{1}{2}$∠AOB=$\frac{1}{2}$α;
(3)∵∠EOB=$\frac{1}{3}$∠COB,
∴∠EOC=$\frac{2}{3}$∠COB,
∴∠EOF=∠EOC+∠COF=$\frac{2}{3}$∠COB+$\frac{2}{3}$∠COA=$\frac{2}{3}$∠BOC+$\frac{2}{3}$∠AOC=$\frac{2}{3}$∠AOB=$\frac{2}{3}$α.
点评 本题考查了角平分线的性质,以及角度的计算,正确理解角平分线的定义是关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
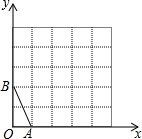 在方格纸中,每个小格的顶点称为格点,以格点的连线为边的三角形称为格点三角形,如图所示的5×5的方格纸中,如果想作格点△ABC与△OAB相似(相似比不能为1),则C点坐标为(4,4)或(5,2).
在方格纸中,每个小格的顶点称为格点,以格点的连线为边的三角形称为格点三角形,如图所示的5×5的方格纸中,如果想作格点△ABC与△OAB相似(相似比不能为1),则C点坐标为(4,4)或(5,2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com