
分析 由多项式x3+ax2+bx+c含有因式x+1和x-1可得x3+ax2+bx+c=(x+1)(x-1)(mx+n),分别令x=±1,可得关于a、b、c的俩方程;再由多项式x3+ax2+bx+c被x-2除余数为3可得x3+ax2+bx+c=p(x-2)+3,令x=2可得关于a、b、c的方程,联立方程组求解可得.
解答 解:∵多项式x3+ax2+bx+c含有因式x+1和x-1,
∴x3+ax2+bx+c=(x+1)(x-1)(mx+n),
当x=1时,1+a+b+c=0,即a+b+c=-1,
当x=-1时,-1+a-b+c=0,即a-b+c=1,
又∵多项式x3+ax2+bx+c被x-2除余数为3,
∴x3+ax2+bx+c=p(x-2)+3,
当x=2时,8+4a+2b+c=3,即4a+2b+c=-5,
联立可得方程组$\left\{\begin{array}{l}{a+b+c=-1}\\{a-b+c=1}\\{4a+2b+c=-5}\end{array}\right.$,
解得:a=-1,b=-1,c=1,
故答案为:-1,-1,1.
点评 本题主要考查因式定理与综合除法的知识点,解答本题的关键是熟练掌握整除带余的概念.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2017届湖北省大冶市九年级3月中考模拟数学试卷(解析版) 题型:解答题
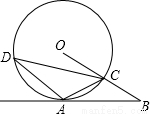
(本小题满分7分) 已知:如图,A是⊙O上一点,半径OC的延长线与过点A的直线交于B点,OC=BC,AC=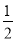 OB.
OB.
(1)求证:AB是⊙O的切线;
(2)若∠ACD=45°,OC=2,求弦CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
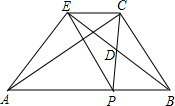 如图,在Rt△ABC中,∠ACB=90°,点P是斜边AB上一个动点(不与A、B重合),连接PC,点D是PC的中点,连接BD并延长至E,使DE=BD,连接EA、EP、EC.
如图,在Rt△ABC中,∠ACB=90°,点P是斜边AB上一个动点(不与A、B重合),连接PC,点D是PC的中点,连接BD并延长至E,使DE=BD,连接EA、EP、EC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
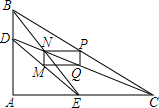 已知:在△ABC中,∠A=90°,D,E分别是AB,AC上任意一点,M,N,P,Q分别是DE,BE,BC,CD的中点,求证:四边形PQMN是矩形.
已知:在△ABC中,∠A=90°,D,E分别是AB,AC上任意一点,M,N,P,Q分别是DE,BE,BC,CD的中点,求证:四边形PQMN是矩形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
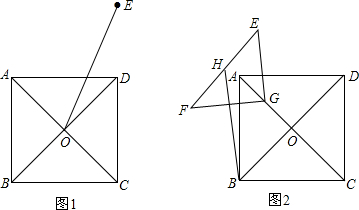
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
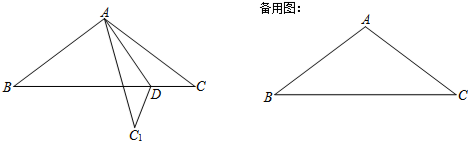
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图为实数a,b在数轴上的位置,则($\sqrt{b}$)2+$\sqrt{(-a)^{2}}$-$\sqrt{(a-b)^{2}}$=0.
如图为实数a,b在数轴上的位置,则($\sqrt{b}$)2+$\sqrt{(-a)^{2}}$-$\sqrt{(a-b)^{2}}$=0.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com