
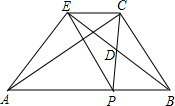
 如图,在Rt△ABC中,∠ACB=90°,点P是斜边AB上一个动点(不与A、B重合),连接PC,点D是PC的中点,连接BD并延长至E,使DE=BD,连接EA、EP、EC.
如图,在Rt△ABC中,∠ACB=90°,点P是斜边AB上一个动点(不与A、B重合),连接PC,点D是PC的中点,连接BD并延长至E,使DE=BD,连接EA、EP、EC.分析 (1)根据对角线互相平分的四边形是平行四边形即可证明.
(2)先证明四边形APCE是平行四边形,再证明PA=PC即可解决问题.
解答 (1)证明:∵D是PC的中点, ∴CD=DP,
∴CD=DP,
又∵DB=DE,
∴四边形PBCE是平行四边形.
(2)∵四边形PCEA不是梯形时,CE∥AP,
∴AE∥PC,
∴四边形AECP是平行四边形,
∴AP=EC,
∵四边形PBCE是平行四边形,
∴EC=PB,
∴AP=BP,
∵∠ACB=90°,
∴PC=PA=PB,
∵四边形PBCE是平行四边形,又PA=PC,
∴四边形APCE是菱形.
故答案分别为=,菱形.
点评 本题考查平行四边形的判定和性质、菱形的判定和性质、直角三角形斜边中线定理等知识,熟练掌握平行四边形、菱形的判定方法是解题的关键,属于中考常考题型.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:解答题
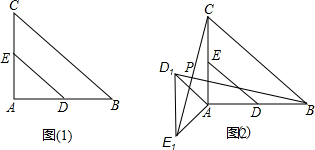 如图(1),在Rt△ABC中,∠A=90°,AC=AB=4,D,E分别是AB,AC的中点.若等腰Rt△ADE绕点A逆时针旋转,得到等腰Rt△AD1E1,如图(2),设旋转角为α(0<α≤180°),记直线BD1与CE1的交点为P.
如图(1),在Rt△ABC中,∠A=90°,AC=AB=4,D,E分别是AB,AC的中点.若等腰Rt△ADE绕点A逆时针旋转,得到等腰Rt△AD1E1,如图(2),设旋转角为α(0<α≤180°),记直线BD1与CE1的交点为P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
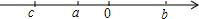 已知实数a,b,c关系是a<0,b>0,c<0,且|c|>|b|>|a|.
已知实数a,b,c关系是a<0,b>0,c<0,且|c|>|b|>|a|.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
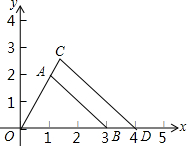 如图,△AOB以O为位似中心,扩大到△COD,各点的坐标分别为A(1,2),B(3,0),D(4,0),求点C的坐标,并求出四边形ABDC的面积.
如图,△AOB以O为位似中心,扩大到△COD,各点的坐标分别为A(1,2),B(3,0),D(4,0),求点C的坐标,并求出四边形ABDC的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
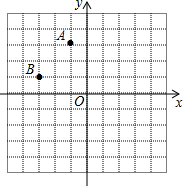 如图,平面直角坐标系中A(-1,3),B(-3,1)
如图,平面直角坐标系中A(-1,3),B(-3,1)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,将△ABC沿BC方向平移3cm得到△DEF,若△ABC的周长为20cm,则四边形ABFD的周长为( )
如图,将△ABC沿BC方向平移3cm得到△DEF,若△ABC的周长为20cm,则四边形ABFD的周长为( )| A. | 20cm | B. | 22cm | C. | 24cm | D. | 26cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com