
【题目】有一科技小组进行了机器人行走性能试验,在试验场地有A、B、C三点顺次在同一笔直的赛道上,A、B两点之间的距离是90米,甲、乙两机器人分别从A、B两点同时同向出发到终点C,乙机器人始终以50米分的速度行走,乙行走9分钟到达C点.设两机器人出发时间为t(分钟),当t=3分钟时,甲追上乙.
请解答下面问题:
(1)B、C两点之间的距离是 米.
(2)求甲机器人前3分钟的速度为多少米/分?
(3)若前4分钟甲机器人的速度保持不变,在4≤t≤6分钟时,甲的速度变为与乙相同,求两机器人前6分钟内出发多长时间相距28米?
(4)若6分钟后甲机器人的速度又恢复为原来出发时的速度,直接写出当t>6时,甲、乙两机器人之间的距离S.(用含t的代数式表示).
![]()
【答案】(1)450;(2)机器人前3分钟的速度为80米/分;(3)两机器人前6分钟内出发![]() 分或
分或![]() 分时相距28米;(4)见解析.
分时相距28米;(4)见解析.
【解析】
(1)根据题目中的数据可以求得B、C两点之间的距离;
(2)根据题意,可以得到甲机器人前3分钟的速度;
(3)根据题意可知前4分钟甲机器人的速度,在4≤t≤6分钟时,甲的速度,从而可以求得两机器人前6分钟内出发多长时间相距28米;
(4)根据题意可以得到当t>6时,甲、乙两机器人之间的距离S.
解:(1)由题意可得,
B、C两点之间的距离是:50×9=450(米),
故答案为:450;
(2)设甲机器人前3分钟的速度为a米/分,
3a=90+3×50,
解得,a=80,
答:机器人前3分钟的速度为80米/分;
(3)∵前4分钟甲机器人的速度保持不变,在4≤t≤6分钟时,甲的速度变为与乙相同,
∴前4分钟甲机器人的速度为80米/分,在4≤t≤6分钟时,甲的速度为50米/分,
设甲乙相遇前相距28米时出发的时间为b分钟,
80b+28=90+50b,
解得,b=![]() ,
,
设甲乙相遇后相距28米时出发的时间为c分钟,
80c﹣28=90+50c,
解得,c=![]() ,
,
答:两机器人前6分钟内出发![]() 分或
分或![]() 分时相距28米;
分时相距28米;
(4)∵6分钟后甲机器人的速度又恢复为原来出发时的速度,
∴6分钟后甲机器人的速度是80米/分,
当t=6时,甲乙两机器人的距离为:[80×4+50×(6﹣2)]﹣(90+50×6)=60(米),
当甲到达终点C时,t={(90+450)﹣[80×4+50×(6﹣2)]}÷80+6=7.5(分),
当乙到达终点C时,t=450÷50=9(分),
∴当6<t≤7.5时,S=60+(80﹣50)×(t﹣6)=30t﹣120,
当7.5<t≤9时,S=450﹣50×7.5﹣50(t﹣7.5)=﹣50t+450,
由上可得,当t>6时,甲、乙两机器人之间的距离S=![]() .
.


 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:
【题目】已知![]() 两地各需220吨和280吨化肥,A市有化肥200吨,B市有化肥300吨,刚好可以全部运往
两地各需220吨和280吨化肥,A市有化肥200吨,B市有化肥300吨,刚好可以全部运往![]() 两地,如果从A市运往
两地,如果从A市运往![]() 两地运价分别为20元/吨和25元/吨,从B市运往
两地运价分别为20元/吨和25元/吨,从B市运往![]() 两地运价分别为15元/吨和22元/吨。
两地运价分别为15元/吨和22元/吨。
(1)如果A市运往C地的化肥为100吨,则总运费共多少元?
(2)设总运费为![]() 元,如果设A市运往C地的化肥
元,如果设A市运往C地的化肥![]() 吨,用含
吨,用含![]() 代数式来表示
代数式来表示![]() ;
;
(3)按照(2)问的要求,猜想![]() 为多少时,总的运费最少,是多少?
为多少时,总的运费最少,是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆某油脂公司生产销售菜籽油、花生油两种食用植物油.
(1)已知花生的出油率为56%,是菜籽的1.4倍,现有菜籽、花生共100吨,若想得到至少52吨植物油,则其中的菜籽至多有多少吨?
(2)在去年的销售中,菜籽油、花生油的售价分别为20元/升,30元/升,且销量相同,今年由于花生原材料价格上涨,花生油的售价比去年提高了a%,菜籽油的售价不变,总销量比去年降低a%,且菜籽油、花生油的销量均占今年总销量的 ![]() ,这样,预计今年的销售总额比去年下降
,这样,预计今年的销售总额比去年下降 ![]() a%,求a的值.
a%,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节三天假期的某一天,小明全家上午8时自驾小汽车从家里出发,到某著名旅游景点游玩.该小汽车离家的距离S(千米)与时间t(小时)的关系如图所示.
(1)在这个过程中,自变量是 ,因变量是 .
(2)景点离小明家多远?
(3)小明一家在景点游玩的时间是多少小时?
(4)小明到家的时间是几点?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线y= ![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,抛物线的顶点为点D,过点B作BC的垂线,交对称轴于点E.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,抛物线的顶点为点D,过点B作BC的垂线,交对称轴于点E.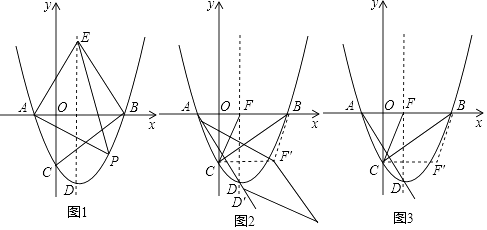
(1)求证:点E与点D关于x轴对称;
(2)点P为第四象限内的抛物线上的一动点,当△PAE的面积最大时,在对称轴上找一点M,在y轴上找一点N,使得OM+MN+NP最小,求此时点M的坐标及OM+MN+NP的最小值;
(3)如图2,平移抛物线,使抛物线的顶点D在射线AD上移动,点D平移后的对应点为D′,点A的对应点A′,设抛物线的对称轴与x轴交于点F,将△FBC沿BC翻折,使点F落在点F′处,在平面内找一点G,若以F′、G、D′、A′为顶点的四边形为菱形,求平移的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=2x与反比例函数y= ![]() 在第一象限内的图象交于点A(m,2),将直线y=2x向下平移4个单位后与反比例函数y=
在第一象限内的图象交于点A(m,2),将直线y=2x向下平移4个单位后与反比例函数y= ![]() 在第一象限内的图象交于点P,则k=;△POA的面积为 .
在第一象限内的图象交于点P,则k=;△POA的面积为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校260名学生参加植树活动,要求每人植4﹣7棵,活动结束后随机抽查了20名学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵,将这四类的人数绘制成扇形图(如图1)和条形图(如图2).
经确认扇形图是正确的,而条形图尚有一处错误.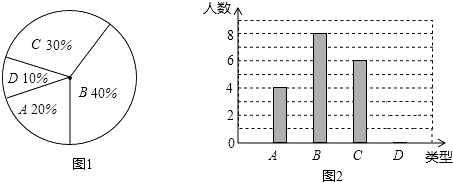
回答下列问题:
(1)写出条形图中存在的错误为;
(2)写出这20名学生每人植树量的众数为;中位数为;
(3)经计算这20名学生每人植树量的平均数为5.3,则估算这260名学生共植树棵.
(4)在这次活动中,九(1)班学生平均每人植6棵树,如果单独由男同学完成,每人应植树15棵,求如果单独由女同学完成,每人应植树多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知BM、CN分别是△![]() 的两个外角的角平分线,
的两个外角的角平分线,![]() 、
、![]() 分别是
分别是![]() 和
和![]() 的角平分线,如图①;
的角平分线,如图①;![]() 、
、![]() 分别是
分别是![]() 和
和![]() 的三等分线(即
的三等分线(即![]() ,
,![]() ),如图②;依此画图,
),如图②;依此画图,![]() 、
、![]() 分别是
分别是![]() 和
和![]() 的n等分线(即
的n等分线(即![]() ,
,![]() ),
),![]() ,且
,且![]() 为整数.
为整数.
(1)若![]()
![]() ,求
,求![]() 的度数;
的度数;
(2)设![]() ,请用
,请用![]() 和n的代数式表示
和n的代数式表示![]() 的大小,并写出表示的过程;
的大小,并写出表示的过程;
(3)当![]() 时,请直接写出
时,请直接写出![]() +
+![]() 与
与![]() 的数量关系.
的数量关系.
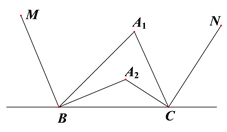
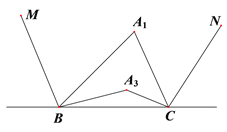
图① 图②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,一天上午6点钟,言老师从学校出发,乘车上市里开会,8点准时到会场,中午12点钟回到学校,他这一段时间内的行程s(km)(即离开学校的距离)与时间(时)的关系可用图中的折线表示,根据图中提供的有关信息,解答下列问题:
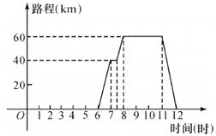
(1)开会地点离学校多远?
(2)请你用一段简短的话,对言老师从上午6点到中午12点的活动情况进行描述.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com