
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌжБЯп![]() ЮЊвЛЁЂШ§ЯѓЯоНЧЦНЗжЯпЃЎЕуPЙигкyжсЕФЖдГЦЕуГЦЮЊPЕФвЛДЮЗДЩфЕуЃЌМЧзї
ЮЊвЛЁЂШ§ЯѓЯоНЧЦНЗжЯпЃЎЕуPЙигкyжсЕФЖдГЦЕуГЦЮЊPЕФвЛДЮЗДЩфЕуЃЌМЧзї![]() ЃЛ
ЃЛ![]() ЙигкжБЯп
ЙигкжБЯп![]() ЕФЖдГЦЕуГЦЮЊЕуPЕФЖўДЮЗДЩфЕуЃЌМЧзї
ЕФЖдГЦЕуГЦЮЊЕуPЕФЖўДЮЗДЩфЕуЃЌМЧзї![]() ЃЎР§ШчЃЌЕу
ЃЎР§ШчЃЌЕу![]() ЕФвЛДЮЗДЩфЕуЮЊ
ЕФвЛДЮЗДЩфЕуЮЊ![]() ЃЌЖўДЮЗДЩфЕуЮЊ
ЃЌЖўДЮЗДЩфЕуЮЊ![]() ЃЎИљОнЖЈвхЃЌЛиД№ЯТСаЮЪЬтЃК
ЃЎИљОнЖЈвхЃЌЛиД№ЯТСаЮЪЬтЃК
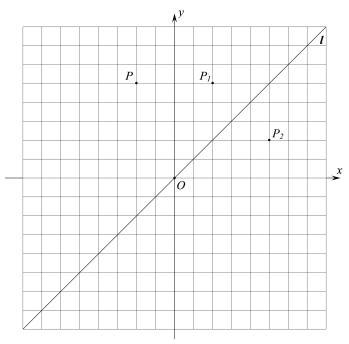
ЃЈ1ЃЉЕу![]() ЕФвЛДЮЗДЩфЕуЮЊ________ЃЌЖўДЮЗДЩфЕуЮЊ__________ЃЛ
ЕФвЛДЮЗДЩфЕуЮЊ________ЃЌЖўДЮЗДЩфЕуЮЊ__________ЃЛ
ЃЈ2ЃЉЕБЕуAдкЕквЛЯѓЯоЪБЃЌЕу![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() жаПЩвдЪЧЕуAЕФЖўДЮЗДЩфЕуЕФЪЧ_________ЃЛ
жаПЩвдЪЧЕуAЕФЖўДЮЗДЩфЕуЕФЪЧ_________ЃЛ
ЃЈ3ЃЉШєЕуAдкЕкЖўЯѓЯоЃЌЕу![]() ЃЌ
ЃЌ![]() ЗжБ№ЪЧЕуAЕФвЛДЮЁЂЖўДЮЗДЩфЕуЃЌЁї
ЗжБ№ЪЧЕуAЕФвЛДЮЁЂЖўДЮЗДЩфЕуЃЌЁї![]() ЮЊЕШБпШ§НЧаЮЃЌЧѓЩфЯпOAгыxжсЫљМаШёНЧЕФЖШЪ§ЃЎ
ЮЊЕШБпШ§НЧаЮЃЌЧѓЩфЯпOAгыxжсЫљМаШёНЧЕФЖШЪ§ЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЌ
ЃЌ![]() ЃЛ ЃЈ2ЃЉNЕуЃЛ ЃЈ3ЃЉЩфЯпOAгыxжсЫљМаШёНЧЮЊ
ЃЛ ЃЈ2ЃЉNЕуЃЛ ЃЈ3ЃЉЩфЯпOAгыxжсЫљМаШёНЧЮЊ![]() Лђ
Лђ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЗДЩфЕФЖЈвхЧѓНтЃЛЃЈ2ЃЉИљОнЗДЩфЖЈвхПЩжЊЕуAЕФЖўДЮЗДЩфЕудкЕкЫФЯоЯюЃЛЃЈ3ЃЉИљОнЗДЩфЖЈвхЕУЕу![]() ОљдкЕквЛЯѓЯоЃЎ Ёї
ОљдкЕквЛЯѓЯоЃЎ Ёї![]() ЮЊЕШБпШ§НЧаЮЃЌ
ЮЊЕШБпШ§НЧаЮЃЌ![]() ЙигкOBЖдГЦЃЌЙЪ
ЙигкOBЖдГЦЃЌЙЪ![]() ЃЛЂйШєЕу
ЃЛЂйШєЕу![]() ЮЛгкжБЯпlЕФЩЯЗНЃЌШчЭМ1ЫљЪОЃЌДЫЪБ
ЮЛгкжБЯпlЕФЩЯЗНЃЌШчЭМ1ЫљЪОЃЌДЫЪБ![]() ЂкШєЕу
ЂкШєЕу![]() ЮЛгкжБЯпlЕФЩЯЯТЗНЃЌШчЭМ2ЫљЪОЃЌДЫЪБ
ЮЛгкжБЯпlЕФЩЯЯТЗНЃЌШчЭМ2ЫљЪОЃЌДЫЪБ![]()
НтЃКЃЈ1ЃЉ![]() ЃЌ
ЃЌ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉNЕуЃЛ
ЃЈ3ЃЉЁпЕуAдкЕкЖўЯѓЯоЃЌ
ЁрЕу![]() ОљдкЕквЛЯѓЯоЃЎ
ОљдкЕквЛЯѓЯоЃЎ
ЁпЁї![]() ЮЊЕШБпШ§НЧаЮЃЌ
ЮЊЕШБпШ§НЧаЮЃЌ![]() ЙигкOBЖдГЦЃЌ
ЙигкOBЖдГЦЃЌ
Ёр![]()
ЗжРрЬжТлЃК
ЂйШєЕу![]() ЮЛгкжБЯпlЕФЩЯЗНЃЌШчЭМ1ЫљЪОЃЌ
ЮЛгкжБЯпlЕФЩЯЗНЃЌШчЭМ1ЫљЪОЃЌ
ДЫЪБ![]()
вђДЫЩфЯпOAгыxжсЫљМаШёНЧЮЊ![]() ЃЛ
ЃЛ
ЂкШєЕу![]() ЮЛгкжБЯпlЕФЩЯЯТЗНЃЌШчЭМ2ЫљЪОЃЌ
ЮЛгкжБЯпlЕФЩЯЯТЗНЃЌШчЭМ2ЫљЪОЃЌ
ДЫЪБ![]()
вђДЫЩфЯпOAгыxжсЫљМаШёНЧЮЊ![]() ЃЛ
ЃЛ
злЩЯЫљЪіЃЌЩфЯпOAгыxжсЫљМаШёНЧЮЊ![]() Лђ
Лђ![]() ЃЎ
ЃЎ

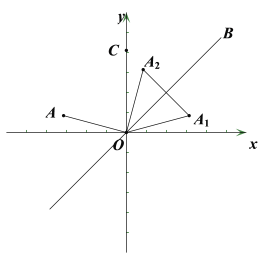
ЭМ1 ЭМ2


 ЦкФЉГхДЬ100ЗжДДаТН№ОэЭъШЋЪдОэЯЕСаД№АИ
ЦкФЉГхДЬ100ЗжДДаТН№ОэЭъШЋЪдОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЪаНЋЪЕааОгУёЩњЛюгУЕчНзЬнЕчМлЗНАИЃЌШчЯТБэЃЌЭМжаелЯпЗДгГСЫУПЛЇОгУёУПдТЕчЗб![]() ЃЈдЊЃЉгыгУЕчСП
ЃЈдЊЃЉгыгУЕчСП![]() ЃЈЖШЃЉМфЕФКЏЪ§ЙиЯЕ.
ЃЈЖШЃЉМфЕФКЏЪ§ЙиЯЕ.
ЕЕДЮ | ЕквЛЕЕ | ЕкЖўЕЕ | ЕкШ§ЕЕ |
УПдТгУЕчСП |
|
|
|
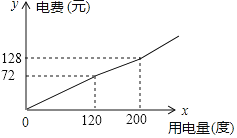
ЃЈ1ЃЉаЁЭѕМвФГдТгУЕч![]() ЖШЃЌашНЛЕчЗб___________дЊЃЛ
ЖШЃЌашНЛЕчЗб___________дЊЃЛ
ЃЈ2ЃЉЧѓЕкЖўЕЕЕчЗб![]() ЃЈдЊЃЉгыгУЕчСП
ЃЈдЊЃЉгыгУЕчСП![]() ЃЈЖШЃЉжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈЖШЃЉжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉаЁЭѕМвФГдТгУЕч![]() ЖШЃЌНЛФЩЕчЗб
ЖШЃЌНЛФЩЕчЗб![]() дЊЃЌЧыФуЧѓГіЕкШ§ЕЕУПЖШЕчЗбБШЕкЖўЕЕУПЖШЕчЗбЖрЖрЩйдЊЃП
дЊЃЌЧыФуЧѓГіЕкШ§ЕЕУПЖШЕчЗбБШЕкЖўЕЕУПЖШЕчЗбЖрЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬШЫОгЊМзЁЂввСНжжЩЬЦЗЃЌУПМўМзжжЩЬЦЗЕФРћШѓТЪЮЊ![]() ЃЌУПМўввжжЩЬЦЗЕФРћШѓТЪЮЊ
ЃЌУПМўввжжЩЬЦЗЕФРћШѓТЪЮЊ![]() ЃЌЕБЪлГіЕФввжжЩЬЦЗЕФМўЪ§БШМзжжЩЬЦЗЕФМўЪ§Жр
ЃЌЕБЪлГіЕФввжжЩЬЦЗЕФМўЪ§БШМзжжЩЬЦЗЕФМўЪ§Жр![]() ЪБЃЌетИіЩЬШЫЕУЕНЕФзмРћШѓТЪЪЧ
ЪБЃЌетИіЩЬШЫЕУЕНЕФзмРћШѓТЪЪЧ![]() ЃЛЕБЪлГіЕФввжжЩЬЦЗЕФМўЪ§БШМзжжЩЬЦЗЕФМўЪ§Щй
ЃЛЕБЪлГіЕФввжжЩЬЦЗЕФМўЪ§БШМзжжЩЬЦЗЕФМўЪ§Щй![]() ЪБЃЌетИіЩЬШЫЕУЕНЕФзмРћШѓТЪЪЧ__________. ЃЈзЂЃКРћШѓТЪ
ЪБЃЌетИіЩЬШЫЕУЕНЕФзмРћШѓТЪЪЧ__________. ЃЈзЂЃКРћШѓТЪ![]() ЃЌзмРћШѓТЪ
ЃЌзмРћШѓТЪ![]() ЃЉ
ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌAB=ACЃЌDЪЧBCБпЩЯЕФЖЏЕуЃЈЕуDгыBЃЌCВЛжиКЯЃЉЃЌЁїABDКЭЁїACDЕФУцЛ§ЗжБ№БэЪОЮЊS1КЭS2ЃЌЯТСаЬѕМўВЛФмЫЕУїADЪЧЁїABCНЧЦНЗжЯпЕФЪЧЃЈ ЃЉ

A.BD=CDB.ЁЯADB=ЁЯADCC.S1=S2D.AD=![]() BC
BC
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖдгкДњЪ§ЪНЃЌВЛЭЌЕФБэДяаЮЪНФмБэЯжГіЫќЕФВЛЭЌаджЪЃЎР§ШчДњЪ§ЪН![]() ЃЌШєНЋЦфаДГЩ
ЃЌШєНЋЦфаДГЩ![]() ЕФаЮЪНЃЌОЭФмПДГіВЛТлзжФИxШЁКЮжЕЃЌЫќЖМБэЪОе§Ъ§ЃЛШєНЋЫќаДГЩ
ЕФаЮЪНЃЌОЭФмПДГіВЛТлзжФИxШЁКЮжЕЃЌЫќЖМБэЪОе§Ъ§ЃЛШєНЋЫќаДГЩ![]() ЕФаЮЪНЃЌОЭФмгыДњЪ§ЪНB=
ЕФаЮЪНЃЌОЭФмгыДњЪ§ЪНB=![]() НЈСЂСЊЯЕЃЎЯТУцЮвУЧИФБфxЕФжЕЃЌбаОПвЛЯТAЃЌBСНИіДњЪ§ЪНШЁжЕЕФЙцТЩЃК
НЈСЂСЊЯЕЃЎЯТУцЮвУЧИФБфxЕФжЕЃЌбаОПвЛЯТAЃЌBСНИіДњЪ§ЪНШЁжЕЕФЙцТЩЃК
x | -2 | -1 | 0 | 1 | 2 | 3 |
| 10 | 5 | 2 | 1 | 5 | |
| 17 | 10 | 5 |
ЃЈ1ЃЉЭъГЩЩЯБэЃЛ
ЃЈ2ЃЉЙлВьБэИёПЩвдЗЂЯжЃК
Шєx=mЪБЃЌ![]() ЃЌдђx=m+1ЪБЃЌ
ЃЌдђx=m+1ЪБЃЌ![]() ЃЎЮвУЧАбетжжЯжЯѓГЦЮЊДњЪ§ЪНAВЮееДњЪ§ЪНBШЁжЕбгКѓЃЌДЫЪБбгКѓжЕЮЊ1ЃЎ
ЃЎЮвУЧАбетжжЯжЯѓГЦЮЊДњЪ§ЪНAВЮееДњЪ§ЪНBШЁжЕбгКѓЃЌДЫЪБбгКѓжЕЮЊ1ЃЎ
ЂйШєДњЪ§ЪНDВЮееДњЪ§ЪНBШЁжЕбгКѓЃЌЯргІЕФбгКѓжЕЮЊ2ЃЌЧѓДњЪ§ЪНDЃЛ
ЂквбжЊДњЪ§ЪН![]() ВЮееДњЪ§ЪН
ВЮееДњЪ§ЪН![]() ШЁжЕбгКѓЃЌЧыжБНгаДГіb-cЕФжЕЃК________ЃЎ
ШЁжЕбгКѓЃЌЧыжБНгаДГіb-cЕФжЕЃК________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
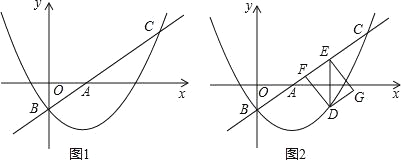
ЁОЬтФПЁПШчЭМ1ЃЌжБЯпlЃКy=![]() x+mгыxжсЁЂyжсЗжБ№НЛгкЕуAКЭЕуBЃЈ0ЃЌЉ1ЃЉЃЌХзЮяЯпy=
x+mгыxжсЁЂyжсЗжБ№НЛгкЕуAКЭЕуBЃЈ0ЃЌЉ1ЃЉЃЌХзЮяЯпy=![]() x2+bx+cОЙ§ЕуBЃЌгыжБЯпlЕФСэвЛИіНЛЕуЮЊCЃЈ4ЃЌnЃЉЃЎ
x2+bx+cОЙ§ЕуBЃЌгыжБЯпlЕФСэвЛИіНЛЕуЮЊCЃЈ4ЃЌnЃЉЃЎ
ЃЈ1ЃЉЧѓnЕФжЕКЭХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕуDдкХзЮяЯпЩЯЃЌDEЁЮyжсНЛжБЯпlгкЕуEЃЌЕуFдкжБЯпlЩЯЃЌЧвЫФБпаЮDFEGЮЊОиаЮЃЈШчЭМ2ЃЉЃЌЩшЕуDЕФКсзјБъЮЊtЃЈ0ЃМtЃМ4ЃЉЃЌОиаЮDFEGЕФжмГЄЮЊpЃЌЧѓpгыtЕФКЏЪ§ЙиЯЕЪНвдМАpЕФзюДѓжЕЃЛ
ЃЈ3ЃЉНЋЁїAOBШЦЦНУцФкФГЕуMа§зЊ90ЁуЛђ180ЁуЃЌЕУЕНЁїA1O1B1ЃЌЕуAЁЂOЁЂBЕФЖдгІЕуЗжБ№ЪЧЕуA1ЁЂO1ЁЂB1ЃЎШєЁїA1O1B1ЕФСНИіЖЅЕуЧЁКУТфдкХзЮяЯпЩЯЃЌФЧУДЮвУЧОЭГЦетбљЕФЕуЮЊЁАТфЕуЁБЃЌЧыжБНгаДГіЁАТфЕуЁБЕФИіЪ§КЭа§зЊ180ЁуЪБЕуA1ЕФКсзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛЗжжгЭЖРКВтЪдЙцЖЈЃКТњЗжЮЊ![]() ЗжЃЌГЩМЈДяЕН
ЗжЃЌГЩМЈДяЕН![]() ЗжМАвдЩЯЮЊКЯИёЃЌГЩМЈДяЕН
ЗжМАвдЩЯЮЊКЯИёЃЌГЩМЈДяЕН![]() ЗжМАвдЩЯЮЊгХауЃЎМзЁЂввСНзщИї
ЗжМАвдЩЯЮЊгХауЃЎМзЁЂввСНзщИї![]() УћбЇЩњЕФФГДЮВтЪдГЩМЈШчЯТЃК
УћбЇЩњЕФФГДЮВтЪдГЩМЈШчЯТЃК
ГЩМЈЃЈЗжЃЉ |
|
|
|
|
|
|
|
|
|
|
МззщЃЈШЫЃЉ |
|
|
|
|
|
|
|
|
|
|
ввзщЃЈШЫЃЉ |
|
|
|
|
|
|
|
|
|
|
![]() ЧыВЙГфЭъГЩЯТУцЕФГЩМЈЗжЮіБэЃК
ЧыВЙГфЭъГЩЯТУцЕФГЩМЈЗжЮіБэЃК
ЭГМЦСП | ЦНОљЗж | ЗНВю | жаЮЛЪ§ | КЯИёТЪ | гХауТЪ |
Мззщ |
|
|
|
| ________ |
ввзщ | ________ |
| ________ |
|
|
![]() ФуШЯЮЊМзЁЂввСНзщФФвЛзщЕФЭЖРКГЩМЈНЯКУЃПЧыаДГіСНЬѕжЇГжФуЕФЙлЕуЕФРэгЩЃЎ
ФуШЯЮЊМзЁЂввСНзщФФвЛзщЕФЭЖРКГЩМЈНЯКУЃПЧыаДГіСНЬѕжЇГжФуЕФЙлЕуЕФРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊвЛДЮКЏЪ§![]() ЃЈ
ЃЈ![]() ЃЌ
ЃЌ![]() ЪЧГЃЪ§ЃЌ
ЪЧГЃЪ§ЃЌ![]() ЃЉЕФЭМЯѓЙ§
ЃЉЕФЭМЯѓЙ§![]() ЃЌ
ЃЌ![]() СНЕу.
СНЕу.
ЃЈ1ЃЉдкЭМжаЛГіИУвЛДЮКЏЪ§ВЂЧѓЦфБэДяЪНЃЛ

ЃЈ2ЃЉШєЕу![]() дкИУвЛДЮКЏЪ§ЭМЯѓЩЯЃЌЧѓ
дкИУвЛДЮКЏЪ§ЭМЯѓЩЯЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ3ЃЉАб![]() ЕФЭМЯѓЯђЯТЦНвЦ3ИіЕЅЮЛКѓЕУЕНаТЕФвЛДЮКЏЪ§ЭМЯѓЃЌдкЭМжаЛГіаТКЏЪ§ЭМаЮЃЌВЂжБНгаДГіаТКЏЪ§ЭМЯѓЖдгІЕФБэДяЪН.
ЕФЭМЯѓЯђЯТЦНвЦ3ИіЕЅЮЛКѓЕУЕНаТЕФвЛДЮКЏЪ§ЭМЯѓЃЌдкЭМжаЛГіаТКЏЪ§ЭМаЮЃЌВЂжБНгаДГіаТКЏЪ§ЭМЯѓЖдгІЕФБэДяЪН.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЈ1ЃЉЃЌPЮЊЁїABCЫљдкЦНУцЩЯвЛЕуЃЌЧвЁЯAPB=ЁЯBPC=ЁЯCPA=120ЁуЃЌдђЕуPНазіЁїABCЕФЗбТэЕуЃЎ
ЃЈ1ЃЉШчЙћЕуPЮЊШёНЧЁїABCЕФЗбТэЕуЃЌЧвЁЯABC=60ЁуЃЎ
ЂйЧѓжЄЃКЁїABPЁзЁїBCPЃЛ
ЂкШєPA=3ЃЌPC=4ЃЌдђPB= ЃЎ
ЃЈ2ЃЉвбжЊШёНЧЁїABCЃЌЗжБ№вдABЁЂACЮЊБпЯђЭтзїе§ЁїABEКЭе§ЁїACDЃЌCEКЭBD ЯрНЛгкPЕуЃЎШчЭМЃЈ2ЃЉ
ЂйЧѓЁЯCPDЕФЖШЪ§ЃЛ
ЂкЧѓжЄЃКPЕуЮЊЁїABCЕФЗбТэЕуЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com