
،¾جâؤ؟،؟بçح¼£¬زرضھ¾طذخABCDضذ£¬AB=4cm£¬BC=6cm£¬¶¯µمP´سµمC؟ھت¼£¬زش1cm/sµؤثظ¶بشعBCµؤرس³¤دكةددٍسزشبثظشث¶¯£¬ء¬½سAP½»CD±كسعµمE£¬°رةندكAPرطض±دكAD·صغ£¬½»CDµؤرس³¤دكسعµمQ£¬ةèµمPµؤشث¶¯ت±¼نخھt£®
£¨1£©بôDQ=3cm£¬اَtµؤضµ£»
£¨2£©ةèDQ=y£¬اَ³ِyسëtµؤ؛¯ت¹طدµت½£»
£¨3£©µ±tخھ؛خضµت±£¬،÷CPEسë،÷AEQµؤأو»دàµب£؟
£¨4£©شع¶¯µمPشث¶¯¹³جضذ£¬،÷APQµؤأو»تا·ٌ»ل·¢ةْ±ن»¯£؟بô±ن»¯£¬اَ³ِ،÷APQµؤأو»S¹طسعtµؤ؛¯ت¹طدµت½£»بô²»±ن£¬ثµأ÷ہيسة£¬²¢اَ³ِSµؤ¶¨ضµ£®
،¾´ً°¸،؟
£¨1£©
½â£؛،كثؤ±كذخABCDخھ¾طذخ£¬
،àCD=AB=4cm£¬
،كAPرطض±دكAD·صغµأµ½AQ£¬
،àQD=DE=3cm£¬
،àCE=CD©پDE=4©پ3=1£¨cm£©£¬
µ±شث¶¯tأëت±£¬شٍPC=tcm£¬
،àBP=£¨t+6£©cm£¬
،كCD،خAB£¬
،à،÷PCE،×،÷PBA£¬
،à ![]() =
= ![]() £¬¼´
£¬¼´ ![]() =
= ![]() £¬
£¬
½âµأt=2
£¨2£©
½â£؛ح¬£¨1£©؟ةضھDE=DQ=y£¬شٍCE=4©پy£¬
ح¬ہي؟ةµأ ![]() =
= ![]() £¬¼´
£¬¼´ ![]() =
= ![]() £¬
£¬
صûہي؟ةµأy= ![]()
£¨3£©
½â£؛²»±ن£¬ہيسةبçدآ£؛
سة£¨2£©؟ةضھµ±CP=tت±£¬QD= ![]() £¬
£¬
شٍQE=2QD= ![]() £¬CE=4©پQD=4©پ
£¬CE=4©پQD=4©پ ![]() =
= ![]() £¬
£¬
،àS،÷AEQ= ![]() QEAD=
QEAD= ![]() ،ء
،ء ![]() ،ء6=
،ء6= ![]() £¬
£¬
S،÷CPE= ![]() CPCE=
CPCE= ![]() ،ءt،ء
،ءt،ء ![]() =
= ![]() £¬
£¬
µ±S،÷CPE=S،÷AEQت±£¬شٍسذ ![]() =
= ![]() £¬
£¬
½âµأt=6 ![]() »ٍt=©پ6
»ٍt=©پ6 ![]() £¨ةلب¥£©£¬
£¨ةلب¥£©£¬
،൱tµؤضµخھ6 ![]() أëت±£¬،÷CPEسë،÷AEQµؤأو»دàµب
أëت±£¬،÷CPEسë،÷AEQµؤأو»دàµب
£¨4£©
½â£؛سة£¨3£©؟ةضھQE= ![]() £¬
£¬
،àS،÷APQ=S،÷AQE+S،÷PQE= ![]() QEAD+
QEAD+ ![]() QECP=
QECP= ![]() QE£¨AD+CP£©=
QE£¨AD+CP£©= ![]() ،ء
،ء ![]() ،ء£¨t+6£©=24£¬
،ء£¨t+6£©=24£¬
،à،÷APQµؤأو»خھ24£¬²»±ن
،¾½âخِ،؟£¨1£©سةصغµ؟ةضھQD=DE£¬؟ةاَµأCE£¬شظہûسأئ½ذذ؟ةµأ،÷PCE،×،÷PBA£¬ہûسأدàثئب½اذخµؤذشضت؟ةµأµ½¹طسعtµؤ·½³ج£¬؟ةاَµأtµؤضµ£»£¨2£©ح¬£¨1£©؟ةسأy±يت¾³ِCE£¬ح¬ہي؟ةہûسأدàثئب½اذخµؤذشضت؟ةµأµ½¹طسعyسëtµؤ؛¯ت¹طدµت½£»£¨3£©ہûسأ£¨2£©ضذµؤ¹طدµت½؟ةسأt±يت¾³ِQE،¢CE£¬شٍ؟ةسأt·ض±ً±يت¾³ِ،÷CPEسë،÷AEQµؤأو»£¬سةأو»دàµب؟ةµأµ½¹طسعtµؤ·½³ج£¬؟ةاَµأt£»£¨4£©سة£¨3£©؟ةسأt·ض±ً±يت¾³ِQE،¢CE£¬؟ة±يت¾³ِ،÷APQµؤأو»خھ¶¨ضµ£®
،¾؟¼µم¾«خِ،؟بدصوةَج⣬ت×دبذèزھءث½âب½اذخµؤأو»(ب½اذخµؤأو»=1/2،ءµ×،ء¸ك)£®


 ح¬²½ء·د°ا؟»¯حطص¹دµءذ´ً°¸
ح¬²½ء·د°ا؟»¯حطص¹دµءذ´ً°¸
| ؤ꼶 | ¸كضذ؟خ³ج | ؤ꼶 | ³ُضذ؟خ³ج |
| ¸كز» | ¸كز»أâ·ر؟خ³جحئ¼ِ£، | ³ُز» | ³ُز»أâ·ر؟خ³جحئ¼ِ£، |
| ¸ك¶ | ¸ك¶أâ·ر؟خ³جحئ¼ِ£، | ³ُ¶ | ³ُ¶أâ·ر؟خ³جحئ¼ِ£، |
| ¸كب | ¸كبأâ·ر؟خ³جحئ¼ِ£، | ³ُب | ³ُبأâ·ر؟خ³جحئ¼ِ£، |
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟زرضھµبرüب½اذخµؤرü³¤خھ6cm£¬µ×±ك³¤خھ4cm£¬زشµبرüب½اذخµؤ¶¥½اµؤ¶¥µمخھش²ذؤ5cmخھ°ë¾¶»ش²£¬ؤاأ´¸أش²سëµ×±كµؤخ»ضأ¹طدµتا£¨ £©
A.دàہë
B.دàاذ
C.دཻ
D.²»ؤـب·¶¨
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟ؤ³ءضزµ²؟أإزھ؟¼²ىؤ³ضضس×ت÷شعز»¶¨جُ¼دآµؤزئض²³ة»îآت£¬شعح¬رùµؤجُ¼دآ¶شصâضضس×ت÷½ّذذ´َء؟زئض²£¬²¢ح³¼ئ³ة»îاé؟ِ£¬¼اآ¼بçدآ£¨ئنضذئµآت½ل¹û±£ءôذ،تµم؛َبخ»£©
زئض²×ـت£¨n£© | 10 | 50 | 270 | 400 | 750 | 1500 | 3500 | 7000 | 9000 |
³ة»îت£¨m£© | 8 | 47 | 235 | 369 | 662 | 1335 | 3203 | 6335 | 8118 |
³ة»îµؤئµآت | 0.800 | 0.940 | 0.870 | 0.923 | 0.883 | 0.890 | 0.915 | 0.905 | 0.902 |
سة´ث؟ةزش¹ہ¼ئس×ت÷زئض²³ة»îµؤ¸إآتخھ £®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟زرضھ¶´خ؛¯ت ![]() £®
£®
£¨1£©اَض¤£؛²»آغkخھبخ؛ختµت£¬¸أ؛¯تµؤح¼دَسëxضل±طسذء½¸ِ½»µم£»
£¨2£©بô¸أ¶´خ؛¯تµؤح¼دَسëxضلµؤء½¸ِ½»µمشعµمA£¨1£¬0£©µؤء½²à£¬از¹طسعxµؤز»شھ¶´خ·½³جk2x2+£¨2k+3£©x+1=0سذء½¸ِ²»دàµبµؤتµت¸ù£¬اَkµؤصûتضµ£»
£¨3£©شع£¨2£©µؤجُ¼دآ£¬¹طسعxµؤءيز»·½³جx2+2£¨a+k£©x+2a©پk2+6k©پ4=0 سذ´َسع0ازذ،سع3µؤتµت¸ù£¬اَaµؤصûتضµ£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟ر§ذ£خھ²خ¼س¸كستتذ،°خهشث»ل،±¹م²¥²ظ±يرف£¬×¼±¸´سئك،¢°ث،¢¾إب¸ِؤ꼶·ض±ًر،ثحµ½خ»µؤز»ؤذ،¢ز»إ®¹²6أû±¸ر،بثضذ£¬أ؟¸ِؤ꼶ثو»ْر،³ِ1أûر§ةْ£¬¹²3أûر§ةْµ£بخءى²ظش±
£¨1£©ر،³ِ3أûءى²ظش±ضذ£¬ؤذةْµؤبثت؟ةؤـتا
£¨2£©اَر،³ِ،°ء½ؤذز»إ®،±3أûءى²ظش±µؤ¸إآت£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼£¬ؤ³ذ£×غ؛دتµ¼ù»î¶¯ذ،×éµؤح¬ر§سû²âء؟¹«ش°ؤعز»؟أت÷DEµؤ¸ك¶ب£¬ثûأاشعصâ؟أت÷صا°·½ز»×ùآ¥ح¤ا°µؤج¨½×ةدAµم´¦²âµأت÷¶¥¶ثDµؤرِ½اخھ30،م£¬³¯×إصâ؟أت÷µؤ·½دٍ×كµ½ج¨½×دآµؤµمC´¦£¬²âµأت÷¶¥¶ثDµؤرِ½اخھ60،م£®زرضھAµمµؤ¸ك¶بABخھ2m£¬ج¨½×ACµؤامذ±½ا،دACBخھ30،م£¬ازB،¢C،¢Eبµمشعح¬ز»جُض±دكةد£®اë¸ù¾فزشةدجُ¼اَ³ِت÷DEµؤ¸ك¶ب£¨²âامئ÷µؤ¸ك¶ب؛ِآش²»¼ئ£©£®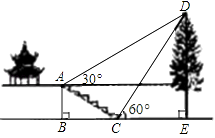
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟تر§»î¶¯؟خةد£¬ہدت¦؛حر§ةْز»ئًب¥²âء؟ر§ذ£ةئىج¨ةدئى¸ثABµؤ¸ك¶ب£®بçح¼£¬ہدت¦²âµأةئىج¨ا°ذ±ئآFCµؤئآ±بخھiFC=1£؛10£¨¼´EF£؛CE=1£؛10£©£¬ر§ةْذ،أ÷ص¾شعہëةئىج¨ث®ئ½¾àہëخھ35m£¨¼´CE=35m£©´¦µؤCµم£¬²âµأئى¸ث¶¥¶ثBµؤرِ½اخھ¦ء£®زرضھtan¦ء= ![]() £¬ةئىج¨¸كAF=1m£¬ذ،أ÷ةي¸كCD=1.6m£¬اë°ïذ،أ÷¼ئثم³ِئى¸ثABµؤ¸ك¶ب£®
£¬ةئىج¨¸كAF=1m£¬ذ،أ÷ةي¸كCD=1.6m£¬اë°ïذ،أ÷¼ئثم³ِئى¸ثABµؤ¸ك¶ب£®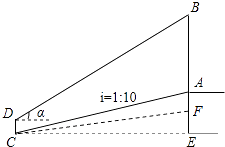
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟،°شھµ©،±ئع¼ن£¬ؤ³ةج³،خھءثخüز¹ث؟ح¹؛خïدû·ر£¬ةè¼ئءثبçح¼ثùت¾µؤز»¸ِ×ھإج£¬×ھإجئ½¾ù·ض³ة3·ف. 
£¨1£©اَ×ھ¶¯¸أ×ھإجز»´خثùµأµؤرصة«تا»ئة«µؤ¸إآت£»
£¨2£©اëسأءذ±ي·¨»ٍ»ت÷×´ح¼µؤ·½·¨ہ´ثµأ÷×ھ¶¯¸أ×ھإجء½´خ£¬ء½´خثùµأµؤرصة«دàح¬µؤ¸إآت.
£¨3£©¸أةج³،ةè¼ئءثبçدآء½ضض½±ہّ·½°¸£؛·½°¸ز»£¬×ھ¶¯¸أ×ھإجز»´خ£¬بô×ھµأµؤرصة«تا»ئة«شٍ؟ةµأ½±£»·½°¸¶£¬×ھ¶¯¸أ×ھإجء½´خ£¬بôء½´خ×ھµأµؤرصة«دàح¬شٍ؟ةµأ½±،£بç¹ûؤمتا¹ث؟ح£¬ؤمر،شٌؤؤضض·½°¸±ب½د»®ثم£؟خھت²أ´£؟
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟ؤ³ذ£ش°خؤر§ةçخھءث½â±¾ذ£ر§ةْ¶ش±¾ةçز»ضض±¨ض½ثؤ¸ِ°وأوµؤد²»¶اé؟ِ£¬ثو»ْ³é²é²؟·ضر§ةْ×ِءثز»´خخت¾يµ÷²é£¬زھاَر§ةْر،³ِ×ش¼؛×îد²»¶µؤز»¸ِ°وأو£¬½«µ÷²éت¾ف½ّذذءثصûہي،¢»وضئ³ة²؟·ضح³¼ئح¼بçدآ£؛
اë¸ù¾فح¼ضذذإد¢£¬½â´ًدآءذختجâ£؛
£¨1£©¸أµ÷²éµؤرù±¾بفء؟خھ £¬ a=%£¬،°µعز»°و،±¶شس¦ةبذخµؤش²ذؤ½اخھ،م£»
£¨2£©اëؤم²¹ب«جُذخح³¼ئح¼£»
£¨3£©بô¸أذ£سذ1000أûر§ةْ£¬اëؤم¹ہ¼ئب«ذ£ر§ةْضذ×îد²»¶،°µعب°و،±µؤبثت£®
²é؟´´ً°¸؛ح½âخِ>>
¹ْ¼تر§ذ£سإر، - ء·د°²لءذ±ي - تشجâءذ±ي
؛±±ت،»¥ءھحّخ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨ئ½ج¨ | حّةدسذ؛¦ذإد¢¾ظ±¨×¨اّ | µçذإص©ئ¾ظ±¨×¨اّ | ةوہْت·ذéخقض÷زهسذ؛¦ذإد¢¾ظ±¨×¨اّ | ةوئَاضب¨¾ظ±¨×¨اّ
خ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨µç»°£؛027-86699610 ¾ظ±¨ستدن£؛58377363@163.com