
【题目】已知点M(3,2),抛物线L:y=x2﹣3x+c与x轴从左到右的交点为A,B.
(1)若抛物线L经过点M(3,2),求抛物线L的解析式和顶点坐标;
(2)当2OA=OB时,求c的值;
(3)直线y=x+b经过点M,与y轴交于点N,①求点N的坐标;②若线段MN与抛物线L:y=x2﹣3x+c有唯一公共点,直接写出正整数c的值.
【答案】(1)y=x2﹣3x+2,顶点坐标为(![]() ,﹣
,﹣![]() );(2)2或﹣18;(3)①(0,﹣1),②1和3
);(2)2或﹣18;(3)①(0,﹣1),②1和3
【解析】
(1)把点M的坐标代入抛物线解析式,利用方程求得c的值;将已得函数解析式配方,可以求得顶点坐标.
(2)设A(![]() ,0),则OB=2OA=2|
,0),则OB=2OA=2|![]() |,需对
|,需对![]() 的正负性进行分类讨论.若
的正负性进行分类讨论.若![]() >0,则B(2
>0,则B(2![]() ,0),根据点A、B关于抛物线对称轴对称可求得
,0),根据点A、B关于抛物线对称轴对称可求得![]() 的值,再把点A坐标代入抛物线解析式,解方程即求得c的值.若
的值,再把点A坐标代入抛物线解析式,解方程即求得c的值.若![]() <0,则B(﹣2
<0,则B(﹣2![]() ,0),计算方法与前面一样.
,0),计算方法与前面一样.
(3)①利用待定系数法确定一次函数解析式,令x=0即求得点N的坐标.
②由于抛物线开口方向、大小,及对称轴固定,可把抛物线看作上下平移,再观察其与线段MN的交点情况.先联立直线MN和抛物线解析式得到关于x的一元二次方程,计算△=0时c的值,把c的值代回方程组求得直线和抛物线此时的交点,落在线段MN上,说明c的值满足条件.把抛物线向下平移,刚好过点M时求出c的值,此时直线与抛物线由两个交点;继续往下平移抛物线,就变成只有一个交点;一直到抛物线经过点N为止,求c的值,于是得到满足条件的c的范围,再取正整数即为所求.
(1)∵抛物线L:y=x2﹣3x+c经过M(3,2)
∴9﹣9+c=2
解得:c=2.
∴y=x2﹣3x+2=(x﹣![]() )2﹣
)2﹣![]()
∴抛物线L的解析式为:y=x2﹣3x+2,顶点坐标为(![]() ,﹣
,﹣![]() )
)
(2)设A(![]() ,0),则OA=|
,0),则OA=|![]() |,OB=2OA=2|
|,OB=2OA=2|![]() |
|
①若![]() >0,则B(2
>0,则B(2![]() ,0)
,0)
∵抛物线对称轴为直线:x=![]() ,点A、B关于对称轴对称
,点A、B关于对称轴对称
∴![]() ,即
,即![]()
解得:![]() =1
=1
∴A(1,0)代入抛物线解析式得:1﹣3+c=0
解得:c=2
②若![]() <0,则B(﹣2
<0,则B(﹣2![]() ,0)
,0)
∴![]()
解得:![]() =﹣3
=﹣3
∴A(﹣3,0)代入抛物线解析式得:9+9+c=0
解得:c=﹣18
综上所述,c的值为2或﹣18.
(3)①∵直线y=x+b经过点M(3,2)
∴3+b=2,解得:b=﹣1
∴直线解析式为y=x﹣1
当x=0时,y=﹣1
∴点N坐标为(0,﹣1)
②联立直线MN与抛物线解析式得:
![]() 整理得:x2﹣4x+c+1=0
整理得:x2﹣4x+c+1=0
当直线与抛物线只有一个交点时,△=(﹣4)2﹣4(c+1)=0
解得:c=3
∴方程的解为: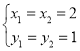
∴此时交点在线段MN上,即c=3满足“线段MN与抛物线L:y=x2﹣3x+c有唯一公共点”
当抛物线经过点M时,解得c=2,此时抛物线与线段MN有2个公共点
当抛物线往下平移到经过点N时,解得c=﹣1,此时抛物线与线段MN只有交点N
∴当﹣1≤c<2时,抛物线与线段MN只有一个公共点
∴满足条件的正整数c的值为1和3.


科目:初中数学 来源: 题型:
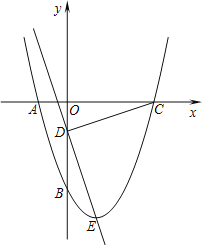
【题目】如图所示,抛物线y=x2+bx+c经过A、B两点,A、B两点的坐标分别为(﹣1,0)、(0,﹣3).
(1)求抛物线的函数解析式;
(2)点E为抛物线的顶点,点C为抛物线与x轴的另一交点,点D为y轴上一点,且DC=DE,求出点D的坐标;
(3)在第二问的条件下,在直线DE上存在点P,使得以C、D、P为顶点的三角形与△DOC相似,请你直接写出所有满足条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
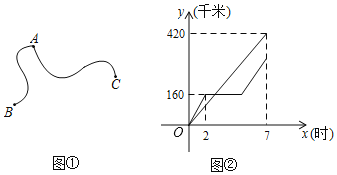
【题目】如图①,甲、乙两车同时从A地出发,分别匀速前往B地与C地,甲车到达B地休息一段时间后原速返回,乙车到达C地后立即返回.两车恰好同时返回A地.图②是两车各自行驶的路程y(千米)与出发时间x(时)之间的函数图象.根据图象解答下列问题:
(1)甲车到达B地休息了 时;
(2)求甲车返回A地途中y与x之间的函数关系式;
(3)当x为何值时,两车与A地的路程恰好相同.(不考虑两车同在A地的情况)
查看答案和解析>>
科目:初中数学 来源: 题型:
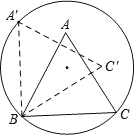
【题目】如图,正△ABC 的边长为 2,顶点 B、C 在半径为![]() 的圆上,顶点 A在圆内,将正△ABC 绕点 B 逆时针旋转,当点 A 第一次落在圆上时,则点 C 运动的路线长为 (结果保留π);若 A 点落在圆上记做第 1 次旋转,将△ABC 绕点 A 逆时针旋转,当点 C 第一次落在圆上记做第 2 次旋转,再绕 C 将△ABC 逆时针旋转,当点 B 第一次落在圆上,记做第 3 次旋转……,若此旋转下去,当△ABC 完成第 2017 次旋转时,BC 边共回到原来位置 次.
的圆上,顶点 A在圆内,将正△ABC 绕点 B 逆时针旋转,当点 A 第一次落在圆上时,则点 C 运动的路线长为 (结果保留π);若 A 点落在圆上记做第 1 次旋转,将△ABC 绕点 A 逆时针旋转,当点 C 第一次落在圆上记做第 2 次旋转,再绕 C 将△ABC 逆时针旋转,当点 B 第一次落在圆上,记做第 3 次旋转……,若此旋转下去,当△ABC 完成第 2017 次旋转时,BC 边共回到原来位置 次.
查看答案和解析>>
科目:初中数学 来源: 题型:
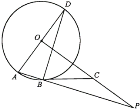
【题目】如图,AD是⊙O的直径,AB为⊙O的弦,OP⊥AD,OP与AB的延长线交于点P,过B点的切线交OP于点C.
(1)求证:∠CBP=∠ADB.
(2)若OA=2,AB=1,求线段BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
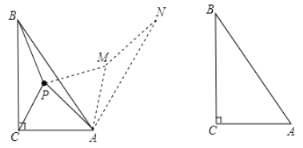
【题目】如图,在![]() 中,
中,![]() ,点P为
,点P为![]() 内一点,连接PA,PB,PC,求PA+PB+PC的最小值,小华的解题思路,以点A为旋转中心,将
内一点,连接PA,PB,PC,求PA+PB+PC的最小值,小华的解题思路,以点A为旋转中心,将![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,那么就将求PA+PB+PC的值转化为求PM+MN+PC的值,连接CN,当点P,M落在CN上时,此题可解.
,那么就将求PA+PB+PC的值转化为求PM+MN+PC的值,连接CN,当点P,M落在CN上时,此题可解.
(1)请判断![]() 的形状,并说明理由;
的形状,并说明理由;
(2)请你参考小华的解题思路,证明PA+PB+PC=PM+MN+PC;
(3)当![]() ,求PA+PB+PC的最小值.
,求PA+PB+PC的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
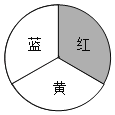
【题目】某商场开业,为了活跃气氛,用红、黄、蓝三色均分的转盘设计了两种抽奖方案,凡来商场消费的顾客都可以选择一种抽奖方案进行抽奖.
方案一:转动转盘一次,指针落在红色区域可领取一份奖品;
方案二:转动转盘两次,指针落在不同颜色区域可领取一份奖品,你会选择哪个方案?请用相关的数学知识说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com