
【题目】如图,在Rt△ABC中,∠C=90°,∠BAC=60°,将△ABC绕点A逆时针旋转60°后得到△ADE,若AC=1,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是(结果保留π).
【答案】![]()
【解析】解:∵∠C=90°,∠BAC=60°,AC=1,
∴AB=2,
扇形BAD的面积是: ![]() =
= ![]() ,
,
在直角△ABC中,BC=ABsin60°=2× ![]() =
= ![]() ,AC=1,
,AC=1,
∴S△ABC=S△ADE= ![]() ACBC=
ACBC= ![]() ×1×
×1× ![]() =
= ![]() .
.
扇形CAE的面积是: ![]() =
= ![]() ,
,
则阴影部分的面积是:S扇形DAB+S△ABC﹣S△ADE﹣S扇形ACE
= ![]() ﹣
﹣ ![]()
= ![]() .
.
故答案为: ![]() .
.
本题考查了扇形的面积的计算,正确理解阴影部分的面积是:S扇形DAB+S△ABC﹣S△ADE﹣S扇形ACE是关键.根据阴影部分的面积是:S扇形DAB+S△ABC﹣S△ADE﹣S扇形ACE , 分别求得:扇形BAD的面积、S△ABC以及扇形CAE的面积,即可求解.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点O为坐标原点,点B的坐标为(4,3),点A、C在坐标轴上,点P在BC边上,直线l1:y=2x+3,直线l2:y=2x﹣3.
(1)分别求直线l1与x轴,直线l2与AB的交点坐标;
(2)已知点M在第一象限,且是直线l2上的点,若△APM是等腰直角三角形,求点M的坐标;
(3)我们把直线l1和直线l2上的点所组成的图形为图形F.已知矩形ANPQ的顶点N在图形F上,Q是坐标平面内的点,且N点的横坐标为x,请直接写出x的取值范围(不用说明理由).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F.若∠B=52°,∠DAE=20°,则∠FED′的大小为 . 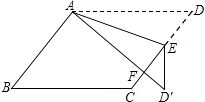
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黔东南州某中学为了解本校学生平均每天的课外学习实践情况,随机抽取部分学生进行问卷调查,并将调查结果分为A,B,C,D四个等级,设学生时间为t(小时),A:t<1,B:1≤t<1.5,C:1.5≤t<2,D:t≥2,根据调查结果绘制了如图所示的两幅不完整的统计图.请你根据图中信息解答下列问题: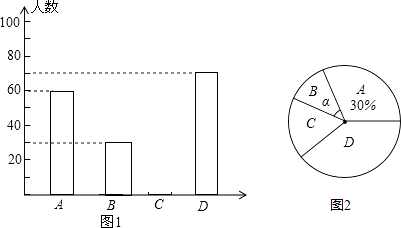
(1)本次抽样调查共抽取了多少名学生?并将条形统计图补充完整;
(2)本次抽样调查中,学习时间的中位数落在哪个等级内?
(3)表示B等级的扇形圆心角α的度数是多少?
(4)在此次问卷调查中,甲班有2人平均每天课外学习时间超过2小时,乙班有3人平均每天课外学习时间超过2小时,若从这5人中任选2人去参加座谈,试用列表或化树状图的方法求选出的2人来自不同班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的一元二次方程x2﹣3x+p=0(p≠0)的两个不相等的实数根分别为a和b,且a2﹣ab+b2=18,则 ![]() +
+ ![]() 的值是( )
的值是( )
A.3
B.﹣3
C.5
D.﹣5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在国务院办公厅发布《中国足球发展改革总体方案》之后,某校为了调查本校学生对足球知识的了解程度,随机抽取了部分学生进行一次问卷调查,并根据调查结果绘制了如图的统计图,请根据图中所给的信息,解答下列问题:
(1)本次接受问卷调查的学生总人数是;
(2)扇形统计图中,“了解”所对应扇形的圆心角的度数为 , m的值为;
(3)若该校共有学生1500名,请根据上述调查结果估算该校学生对足球的了解程度为“基本了解”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一次数学课外实践活动中,小聪在距离旗杆10m的A处测得旗杆顶端B的仰角为60°,测角仪高AD为1m,则旗杆高BC为 m(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB,添加一个条件,不能使四边形DBCE成为矩形的是( ) 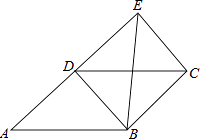
A.AB=BE
B.BE⊥DC
C.∠ADB=90°
D.CE⊥DE
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com