
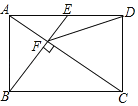
【题目】如图,点E是矩形ABCD的边AD的中点,且BE⊥AC于点F,则下列结论中错误的是( )
A.AF=![]() CF
CF
B.∠DCF=∠DFC
C.图中与△AEF相似的三角形共有5个
D.tan∠CAD=![]()
【答案】D
【解析】
由AE=![]() AD=
AD=![]() BC,又AD∥BC,所以
BC,又AD∥BC,所以![]() ,故A正确,不符合题意;
,故A正确,不符合题意;
过D作DM∥BE交AC于N,得到四边形BMDE是平行四边形,求出BM=DE=![]() BC,得到CN=NF,根据线段的垂直平分线的性质可得结论,故B正确,不符合题意;
BC,得到CN=NF,根据线段的垂直平分线的性质可得结论,故B正确,不符合题意;
根据相似三角形的判定即可求解,故C正确,不符合题意;
由△BAE∽△ADC,得到CD与AD的大小关系,根据正切函数可求tan∠CAD的值,故D错误,符合题意.
解:A、∵AD∥BC,
∴△AEF∽△CBF,
∴![]() =
=![]() ,
,
∵AE=![]() AD=
AD=![]() BC,
BC,
∴![]() =
=![]() ,故A正确,不符合题意;
,故A正确,不符合题意;
B、过D作DM∥BE交AC于N,
∵DE∥BM,BE∥DM,
∴四边形BMDE是平行四边形,
∴BM=DE=![]() BC,
BC,
∴BM=CM,
∴CN=NF,
∵BE⊥AC于点F,DM∥BE,
∴DN⊥CF,
∴DF=DC,
∴∠DCF=∠DFC,故B正确,不符合题意;
C、图中与△AEF相似的三角形有△ACD,△BAF,△CBF,△CAB,△ABE共有5个,故C正确,不符合题意.
D、设AD=a,AB=b由△BAE∽△ADC,有![]() =
=![]() .
.
∵tan∠CAD=![]() =
=![]() =
=![]() ,故D错误,符合题意.
,故D错误,符合题意.
故选:D.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
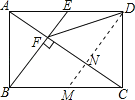
【题目】如图,在梯形ABCD中,AD // BC,AB = CD,AD = 5,BC = 15,![]() .E为射线CD上任意一点,过点A作AF // BE,与射线CD相交于点F.联结BF,与直线AD相交于点G.设CE = x,
.E为射线CD上任意一点,过点A作AF // BE,与射线CD相交于点F.联结BF,与直线AD相交于点G.设CE = x,![]() .
.
(1)求AB的长;
(2)当点G在线段AD上时,求y关于x的函数解析式,并写出函数的定义域;
(3)如果![]() ,求线段CE的长.
,求线段CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
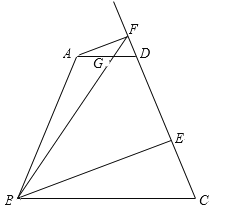
【题目】如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
(1)请在网格中建立平面直角坐标系,使A点坐标为(-2,4),B点坐标为(-4,2);
(2)在第二象限内的格点(网格线的交点)上画一点C,使点C与线段AB组成一个以AB为底的等腰三角形,且腰长是无理数,求C点坐标和△ABC的周长(结果保留根号);
(3)画出△ABC以点C为旋转中心,旋转180°后的△DEC,连结AE和BD,试说明四边形ABDE是什么特殊四边形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两人在相同条件下完成了10次射击训练,两人的成绩如图所示。

根据以上信息,整理分析数据如下:
平均成绩/环 | 中位数/环 | 方差/环 | |
甲 | ______ | 7 | 1.2 |
乙 | 7 | ______ | ______ |
(1)完成表格;
(2)根据训练成绩,你认为选派哪一名队员参赛更好?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一张半径为![]() 的圆形纸片,点
的圆形纸片,点![]() 为圆心,将该圆形纸片沿直线
为圆心,将该圆形纸片沿直线![]() 折叠,直线
折叠,直线![]() 交
交![]() 于
于![]() 两点.
两点.
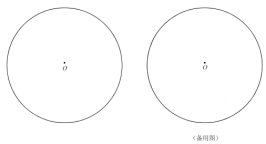
(1)若折叠后的圆弧恰好经过点![]() ,利用直尺和圆规在图中作出满足条件的一条直线
,利用直尺和圆规在图中作出满足条件的一条直线![]() (不写作法,保留作图痕迹),并求此时线段
(不写作法,保留作图痕迹),并求此时线段![]() 的长度.
的长度.
(2)已知![]() 是
是![]() 一点,
一点,![]() .
.
①若折叠后的圆弧经过点![]() ,则线段
,则线段![]() 长度的取值范围是________.
长度的取值范围是________.
②若折叠后的圆弧与直线![]() 相切于点
相切于点![]() ,则线段
,则线段![]() 的长度为_________
的长度为_________![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有分别标有数字-3、-1、0、2的四个小球,除数字不同外,小球没有任何区别,每次试验先搅拌均匀.
(1)从中任取一球,将球上的数字记为a,则关于x的元二次方程x2-2x-a+1=0有实数根的概率______;
(2)从中任取一球,将球上的数字作为点的横坐标,记为x(不放回);再任取一球,将球上的数字作为点的纵坐标,记为y,试用画树状图(或列表法)表示出点(x,y)所有可能出现的结果,并求点(x,y)落在第三象限内的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠ABC=30°,△CDE是等边三角形,点D在边AB上.

(1)如图1,当点E在边BC上时,求证DE=EB;
(2)如图2,当点E在△ABC内部时,猜想ED和EB数量关系,并加以证明;
(3)如图3,当点E在△ABC外部时,EH⊥AB于点H,过点E作GE∥AB,交线段AC的延长线于点G,AG=5CG,BH=3.求CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
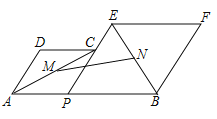
【题目】如图,已知![]() ,
,![]() 为线段
为线段![]() 上的一个动点,分别以
上的一个动点,分别以![]() ,
,![]() 为边在
为边在![]() 的同侧作菱形
的同侧作菱形![]() 和菱形
和菱形![]() .点
.点![]() ,
,![]() ,
,![]() 在一条直线上,
在一条直线上,![]() ,
,![]() 、
、![]() 分别是对角线
分别是对角线![]() 、
、![]() 的中点.当点
的中点.当点![]() 在线段
在线段![]() 上移动时,点
上移动时,点![]() 、
、![]() 之间的距离最短为_______.
之间的距离最短为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
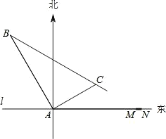
【题目】在某飞机场东西方向的地面 l 上有一长为 1km 的飞机跑道 MN(如图),在跑道 MN的正西端 14.5 千米处有一观察站 A.某时刻测得一架匀速直线降落的飞机位于点 A 的北偏西30°,且与点 A 相距 15 千米的 B 处;经过 1 分钟,又测得该飞机位于点 A 的北偏东 60°,且与点 A 相距 5![]() 千米的 C 处.
千米的 C 处.
(1)该飞机航行的速度是多少千米/小时?(结果保留根号)
(2)如果该飞机不改变航向继续航行,那么飞机能否降落在跑道 MN 之间?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com