
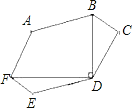
【题目】如图所示,六边ABCDEF中,AB平行且等于ED,AF平行且等于CD,BC平行且等于FE,对角线FD⊥BD.已知FD=24![]() ,BD=18
,BD=18![]() .则六边形ABCDEF的面积是______.
.则六边形ABCDEF的面积是______.
科目:初中数学 来源: 题型:
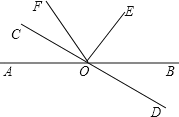
【题目】如图,直线![]() 、
、![]() 相交于
相交于![]() ,∠EOC=90°,
,∠EOC=90°,![]() 是
是![]() 的角平分线,
的角平分线,![]() ,求
,求![]() 的度数.其中一种解题过程如下:请在括号中注明根据,在横线上补全步骤.
的度数.其中一种解题过程如下:请在括号中注明根据,在横线上补全步骤.
解:∵![]()
![]() ( )
( )
∴![]()
![]()
∵![]() 是
是![]() 的角平分线
的角平分线
∴![]()
![]() ( )
( )
∴![]()
![]()
∵![]()
![]()
![]() ( )
( )
∴![]()
![]() ( )
( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图![]() 为奇数排成的数表,用十字框任意框出
为奇数排成的数表,用十字框任意框出![]() 个数,记框内中间这个数为
个数,记框内中间这个数为![]() ,其它四个数分别记为
,其它四个数分别记为![]() ,
,![]() ,
,![]() ,
,![]() (如图
(如图![]() );图
);图![]() 为按某一规律排成的另一个数表,用十字框任意框出
为按某一规律排成的另一个数表,用十字框任意框出![]() 个数,记框内中间这个数为
个数,记框内中间这个数为![]() ,其它四个数记为
,其它四个数记为![]() ,
,![]() ,
,![]() ,
,![]() (如图
(如图![]() ).
).
(1)请你含![]() 的代数式表示
的代数式表示![]() .
.
(2)请你含![]() 的代数式表示
的代数式表示![]() .
.
(3)若![]() ,
,![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为4的正方形ABCD中,P是BC边上一动点(不含B、C点).将△ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的有_____________(写出所有正确结论的序号).
①∠N\AF=45°;②当P为 BC中点时,AE为线段NP的中垂线;
③四边形AMCB的面积最大值为10; ④线段AM的最小值为2![]() ;
;
⑤当△ABP≌△ADN时,BP=4![]() -4.
-4.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知O为圆锥的顶点,M为圆锥底面上一点,点P在OM上.一只蜗牛从P点出发,绕圆锥侧面爬行,回到P点时所爬过的最短路线的痕迹如图所示.若沿OM将圆锥侧面剪开并展开,所得侧面展开图是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
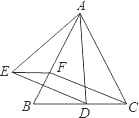
【题目】如图,已知△ABC是等边三角形,点D、F分别在线段BC、AB上,∠EFB=60°,DC=EF.
(1)求证:四边形EFCD是平行四边形;
(2)若BF=EF,求证:AE=AD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解我市市区初中生“绿色出行”方式的情况,某初中数学兴趣小组以问卷调查的形式,随机调查了本校部分学生上下学的主要出行方式,并将调查结果绘制了如图所示的两幅不完整的统计图,请根据图中提供的信息解答以下问题:
种类 |
|
|
|
|
|
出行方式 | 步行 | 公交车 | 自行车 | 私家车 | 出租车 |
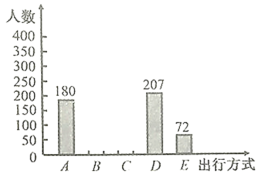
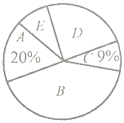
(1)参与本次问卷调查的学生共有_________人,其中选择![]() 类的人数所占的百分比为____________.
类的人数所占的百分比为____________.
(2)请通过计算补全条形统计图,并计算扇形统计图中![]() 类所对应扇形的圆心角的度数.
类所对应扇形的圆心角的度数.
(3)我市市区初中生每天约![]() 人出行,若将
人出行,若将![]() ,
,![]() ,
,![]() 这三类出行方式均视为“绿色出行”方式,请估计我市市区初中生选取“绿色出行”方式的人数.
这三类出行方式均视为“绿色出行”方式,请估计我市市区初中生选取“绿色出行”方式的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
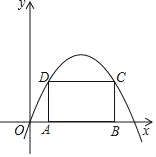
【题目】如图,A,B两点在x轴的正半轴上运动,四边形ABCD是矩形,C,D两点在抛物线y=﹣x2+8x上.
(1)若OA=1,求矩形ABCD的周长;
(2)设OA=m(0<m<4),求出四边形ABCD的周长L关于m的函数表达式;
(3)在(2)的条件下求L的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
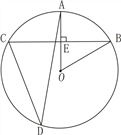
【题目】如图,在⊙O 中,BC是弦,OA⊥BC于点E,D为⊙O上一点,连接AD,CD.
(1)求证:∠AOB=2∠ADC;
(2)若OB⊥CD,CD=8,OE=![]() ,求tan∠ADC.
,求tan∠ADC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com