Question

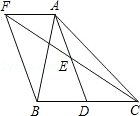
【题目】如图，在△ABC中，D是BC边上的一点，E是AD的中点，过A点作BC的平行线交CE的延长线于点F，且AF=BD，连接BF．
（1）求证：BD=CD；
（2）如果AB=AC，试判断四边形AFBD的形状，并证明你的结论．

Answer 1

【答案】
（1）证明：

∵AF∥BC，

∴∠AFE=∠DCE，

∵E是AD的中点，

∴AE=DE，

，

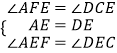∴△AEF≌△DEC（AAS），

∴AF=DC，

∵AF=BD，

∴BD=CD

（2）证明：四边形AFBD是矩形．

理由：

∵AB=AC，D是BC的中点，

∴AD⊥BC，

∴∠ADB=90°

∵AF=BD，

∵过A点作BC的平行线交CE的延长线于点F，即AF∥BC，

∴四边形AFBD是平行四边形，

又∵∠ADB=90°，

∴四边形AFBD是矩形．

【解析】（1）先由AF∥BC，利用平行线的性质可证∠AFE=∠DCE，而E是AD中点，那么AE=DE，∠AEF=∠DEC，利用AAS可证△AEF≌△DEC，那么有AF=DC，又AF=BD，从而有BD=CD；（2）四边形AFBD是矩形．由于AF平行等于BD，易得四边形AFBD是平行四边形，又AB=AC，BD=CD，利用等腰三角形三线合一定理，可知AD⊥BC，即∠ADB=90°，那么可证四边形AFBD是矩形．