
【题目】二次函数![]() =
=![]() +
+![]() +
+![]() 的顶点M是直线
的顶点M是直线![]() =-
=-![]() 和直线
和直线![]() =
=![]() +
+![]() 的交点.
的交点.
(1)若直线![]() =
=![]() +
+![]() 过点D(0,-3),求M点的坐标及二次函数
过点D(0,-3),求M点的坐标及二次函数![]() =
=![]() +
+![]() +
+![]() 的解析式;
的解析式;
(2)试证明无论![]() 取任何值,二次函数
取任何值,二次函数![]() =
=![]() +
+![]() +
+![]() 的图象与直线
的图象与直线![]() =
=![]() +
+![]() 总有两个不同的交点;
总有两个不同的交点;
(3)在(1)的条件下,若二次函数![]() =
=![]() +
+![]() +
+![]() 的图象与
的图象与![]() 轴交于点C,与
轴交于点C,与![]() 的右交点为A,试在直线
的右交点为A,试在直线![]() =-
=-![]() 上求异于M的点P,使P在△CMA的外接圆上.
上求异于M的点P,使P在△CMA的外接圆上.
【答案】(1)M点坐标为M(2,-1),二次函数![]() =
=![]() +
+![]() +
+![]() 的解析式为:
的解析式为: ![]() =
=![]() -4
-4![]() +3;
+3;
(2)证明见解析;
(3)P(-![]() ,
, ![]() )
)
【解析】(本小题满分14分)
解:(1)把D(0,-3)坐标代入直线![]() =
=![]() +
+![]() 中,
中,
得![]() =-3,从而得直线
=-3,从而得直线![]() =
=![]() -3.……………………………………………1分
-3.……………………………………………1分
由M为直线![]() =-
=-![]() 与直线
与直线![]() =
=![]() -3的交点,
-3的交点,
得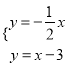 ,………………………………………………………………………2分
,………………………………………………………………………2分
解得![]() ,∴得M点坐标为M(2,-1).…………………………………3分
,∴得M点坐标为M(2,-1).…………………………………3分
∵M为二次函数![]() =
=![]() +
+![]() +
+![]() 的顶点,∴其对称轴为
的顶点,∴其对称轴为![]() =2,
=2,
由对称轴公式: ![]() =-
=-![]() ,得-
,得-![]() =2,∴
=2,∴![]() =-4;
=-4;
由![]() =-1,得
=-1,得![]() =-1,得
=-1,得![]() =3.
=3.
∴二次函数![]() =
=![]() +
+![]() +
+![]() 的解析式为:
的解析式为: ![]() =
=![]() -4
-4![]() +3;………………4分
+3;………………4分
[也可用顶点式求得解析式:由M(2,-1),
得![]() =
=![]() -1,展开得
-1,展开得![]() =
=![]() -4
-4![]() +3]
+3]
(2)∵M是直线![]() =-
=-![]() 和
和![]() =
=![]() +
+![]() 的交点,得
的交点,得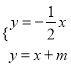 ,
,
解得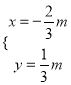 ,∴得M点坐标为M(-
,∴得M点坐标为M(-![]() ,
, ![]() ).…………………………1分
).…………………………1分
从而有-![]() =-
=-![]() 和
和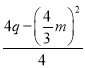 =
=![]() ,
,
解得![]() =
=![]() ;
; ![]() =
=![]() +
+![]() .…………………………………………………3分
.…………………………………………………3分
由![]() ,得
,得![]() +(
+(![]() -1)
-1)![]() +
+![]() -
-![]() =0,……………………4分
=0,……………………4分
该一元二次方程根的判别式
⊿=(![]() -1)2-4(
-1)2-4(![]() -
-![]() )
)
=(![]() -1)2-4(
-1)2-4(![]() +
+![]() -
-![]() )=1>0,…………………………5分
)=1>0,…………………………5分
∴二次函数![]() =
=![]() +
+![]() +
+![]() 的图象与直线
的图象与直线![]() =
=![]() +
+![]() 总有两个不同的交点;
总有两个不同的交点;
(3)解法①:
由(1)知,二次函数的解析式为: ![]() =
=![]() -4
-4![]() +3,
+3,
当![]() =0时,
=0时, ![]() =3.∴点C的坐标为C(0,3).……………………………1分
=3.∴点C的坐标为C(0,3).……………………………1分
令![]() =0,即
=0,即![]() -4
-4![]() +3=0,解得
+3=0,解得![]() =1,
=1, ![]() =3,
=3,
∴点A的坐标为A(3,0).………………………………………………………2分
由勾股定理,得AC=3![]() .∵M点的坐标为M(2,-1),
.∵M点的坐标为M(2,-1),
过M点作![]() 轴的垂线,垂足的坐标应为(2,0),由勾股定理,
轴的垂线,垂足的坐标应为(2,0),由勾股定理,
得AM=![]() ;过M点作
;过M点作![]() 轴的垂线,垂足的坐标应为(0,-1),
轴的垂线,垂足的坐标应为(0,-1),
由勾股定理,得CM=![]() =
=![]() =2
=2![]() .
.
∵AC2+AM2=20=CM2,∴△CMA是直角三角形,……………………3分
CM为斜边,∠CAM=90°.
直线![]() =-
=-![]() 与△CMA的外接圆的一个交点为M,另一个交点为P,
与△CMA的外接圆的一个交点为M,另一个交点为P,
则∠CPM=90°.即△CPM为Rt△.………………………………………4分
设P点的横坐标为![]() ,则P(
,则P(![]() ,-
,- ![]() ).过点P作
).过点P作![]() 轴垂线,
轴垂线,
过点M作![]() 轴垂线,两条垂线交于点E(如图4),则E(
轴垂线,两条垂线交于点E(如图4),则E(![]() ,-1).
,-1).
过P作PF⊥![]() 轴于点F,则F(0,-
轴于点F,则F(0,- ![]() ).
).
在Rt△PEM中,PM2=PE2+EM2
=(-![]() +1)2+(2-
+1)2+(2-![]() )2=
)2=![]() -5
-5![]() +5.
+5.
在Rt△PCF中,PC2=PF2+CF2=![]() +(3+
+(3+![]() )2
)2
=![]() +3
+3![]() +9.在Rt△PCM中,PC2+PM2=CM2,
+9.在Rt△PCM中,PC2+PM2=CM2,
得![]() +3
+3![]() +9+
+9+![]() -5
-5![]() +5=20,
+5=20,
化简整理得5![]() -4
-4![]() -12=0,解得
-12=0,解得![]() =2,
=2, ![]() =-
=-![]() .
.
当![]() =2时,
=2时, ![]() =-1,即为M点的横、纵坐标.
=-1,即为M点的横、纵坐标.
∴P点的横坐标为-![]() ,纵坐标为
,纵坐标为![]() .
.
∴P(-![]() ,
, ![]() ).……………………………………………………………………5分
).……………………………………………………………………5分
解法②[运用现行高中基本知识(解析几何):线段中点公式及两点间距离公式]:
设线段CM的中点(即△CMA内接圆的圆心)为H,则由线段中点公式,可求出H的坐标为H(1,1).∵点P在⊙H上,∴点P到圆心H的距离等于半径.
设点P的坐标为:P(![]() ,-
,- ![]() ),由两点间的距离公式,得PH的长度为:
),由两点间的距离公式,得PH的长度为:
 ,从而有:
,从而有: 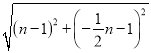 =
=![]() ,即
,即
![]() =5,化简,整理,得化简整理得5
=5,化简,整理,得化简整理得5![]() -4
-4![]() -12=0,解得
-12=0,解得![]() =2,
=2, ![]() =-
=-![]() .当
.当![]() =2时,
=2时, ![]() =-1,即为M点的横、纵坐标.
=-1,即为M点的横、纵坐标.
∴P点的横坐标为-![]() ,纵坐标为
,纵坐标为![]() .
.
∴P(-![]() ,
, ![]() ).
).


 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
【题目】已知两个正数a,b,可按规则c=ab+a+b扩充为一个新数c,在a,b,c三个数中取两个较大的数,按上述规则扩充得到一个新数,依次下去,将每扩充一次得到一个新数称为一次操作。
(1)若a=1,b=3,按上述规则操作3次,扩充所得的数是__________;
(2)若p>q>0,经过3次操作后扩充所得的数为![]() (m,n为正整数),则m,n的值分别为__________.
(m,n为正整数),则m,n的值分别为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
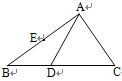
【题目】如图,△ABC中,D为BC边上的点,∠CAD=∠CDA,E为AB边的中点.
(1)尺规作图:作∠C的平分线CF,交AD于点F(保留作图痕迹,不写作法);
(2)连结EF,EF与BC是什么位置关系?为什么?
(3)若四边形BDFE的面积为9,求△ABD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文艺团体为“希望工程”募捐组织了一场义演,共售出1000张票,筹出票款6920元,且每张成人票8元,学生票5元.
(1)问成人票与学生票各售出多少张?
(2)若票价不变,仍售出1000张票,所得的票款可能是7290元吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
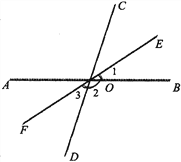
【题目】如图所示,直线AB、CD相交于点O,且∠BOC=80°,OE平分∠BOC.OF为OE的反向延长线.求∠2和∠3的度数,并说明OF是否为∠AOD的平分线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com