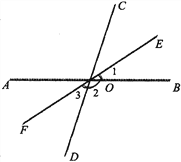
【题目】如图所示，直线AB、CD相交于点O，且∠BOC＝80°，OE平分∠BOC．OF为OE的反向延长线．求∠2和∠3的度数，并说明OF是否为∠AOD的平分线．

参考答案：

【答案】∠2=100°；∠3=40°；OF平分∠AOD，理由见解析.

【解析】试题分析：根据∠BOC的度数以及∠BOC与∠2互补，从而求出∠2的度数；根据OE为角平分线求出∠1的度数，然后根据∠1+∠2+∠3=180°求出∠3的度数；根据∠AOF+∠2+∠3=180°求出∠AOF的度数，最后根据∠AOF=∠3得出答案．

试题解析：∵∠BOC+∠2=180°，∠BOC=80°，
∴∠2=180°-80°=100°；
∵OE是∠BOC的角平分线，
∴∠1=40°．
∵∠1+∠2+∠3=180°，
∴∠3=180°-∠1-∠2=180°-40°-100°=40°．

∵∠2+∠3+∠AOF=180°，
∴∠AOF=180°-∠2-∠3=180°-100°-40°=40°．
∴∠AOF=∠3=40°，
∴OF平分∠AOD．

关闭