【题目】按要求解答：
（1）计算： 
；
（2）因式分解： 
；
（3）先化简，再求值： 
，其中 
.
【答案】
（1）
（2）
解：a2-ab
=a（a-b）
（3）
解：（x+2）2-x（x-2）
由 
得，原式 
【解析】（1）根据零指数次幂和负整数次幂计算；
（2）利用提公因式法分解因式，注意检查分解到不能再分解为止；
（3）利用完全平方公式和整式的混合运算化简求值即可.
【考点精析】通过灵活运用零指数幂法则和整数指数幂的运算性质，掌握零次幂和负整数指数幂的意义： a0=1（a≠0）;a-p=1/ap（a≠0，p为正整数）；aman=am+n(m、n是正整数)；（am）n=amn(m、n是正整数)；(ab)n=anbn(n是正整数)；am/an=am-n(a不等于0，m、n为正整数）；（a/b）n=an/bn(n为正整数)即可以解答此题．
全优考典单元检测卷及归类总复习系列答案科目：初中数学 来源： 题型：
【题目】如图，已知线段AB，按下列要求完成画图和计算：
(1)延长线段AB到点C，使BC＝2AB，取AC中点D；
(2)在(1)的条件下，如果AB＝4，求线段BD的长度．
查看答案和解析>>
科目：初中数学 来源： 题型：
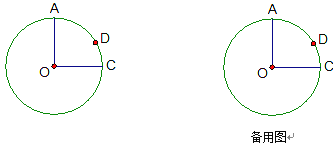
【题目】如图，⊙O的半径OA⊥OC，点D在
上，且
＝2
，OA＝4．
（1）∠COD＝ °；
（2）求弦AD的长；
（3）P是半径OC上一动点，连结AP、PD，请求出AP＋PD的最小值，并说明理由．
（解答上面各题时，请按题意，自行补足图形）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】二次函数
＝
＋
＋
的顶点Ｍ是直线
＝－
和直线
＝
＋
的交点．
（1）若直线
＝
＋
过点D（0，－3），求M点的坐标及二次函数
＝
＋
＋
的解析式；
（2）试证明无论
取任何值，二次函数
＝
＋
＋
的图象与直线
＝
＋
总有两个不同的交点；
（3）在（1）的条件下，若二次函数
＝
＋
＋
的图象与
轴交于点C，与
的右交点为A，试在直线
＝－
上求异于M的点P，使P在△CMA的外接圆上．
查看答案和解析>>
科目：初中数学 来源： 题型：
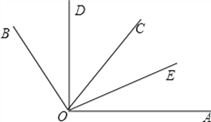
【题目】如图，OD平分∠BOC，OE平分∠AOC．若∠BOC=70°，∠AOC=50°．
（1）求出∠AOB及其补角的度数；
（2）请求出∠DOC和∠AOE的度数，并判断∠DOE与∠AOB是否互补，并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com