练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    10．计算：（$\frac{\sqrt{3}}{3}$）-2-|$\root{3}{-8}$+$\sqrt{3}$|×（-$\frac{4}{\sqrt{12}}$）

    分析 根据负指数幂、绝对值、二次根式的化简解答．

    解答 解：原式=$\frac{1}{（\frac{\sqrt{3}}{3}）^{2}}$-|-2+$\sqrt{3}$|×（-$\frac{2}{\sqrt{3}}$）
    =3-（2-$\sqrt{3}$）×（-$\frac{2}{\sqrt{3}}$）
    =3+（$\frac{4}{\sqrt{3}}$-2）
    =3+$\frac{4\sqrt{3}}{3}$-2
    =1+$\frac{4\sqrt{3}}{3}$
    =$\frac{3+4\sqrt{3}}{3}$．

    点评 本题考查实数的运算，是各地中考题中常见的计算题型．解决此类题目的关键是熟练掌握负整数指数幂、二次根式、绝对值等考点的运算．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

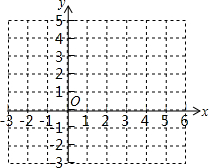    20．已知直线y1=x+b与抛物线y2=-x2+ax+c的一个交点为（2，3），且x=1为该抛物线的对称轴．
    （1）求直线y1=x+b的解析式和抛物线y2=-x2+ax+c的顶点坐标；
    （2）在给出的坐标系中画出直线y1=x+b及抛物线y2=-x2+ax+c的图象，并根据图象，直接写出使得y1≤y2的取值范围；
    （3）设抛物线于x轴的右边交点为A，过点A作x轴的垂线，交直线y1=x+b于点B，点P在抛物线上，当S△PAB≤6时，求点P的横坐标x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

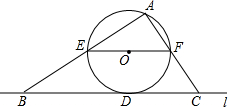    1．如图，直线L与⊙O相切于点D．过圆心O作EF∥L交⊙O于E、F两点，点A是⊙O上一点，连接AE、AF．并分别延长交直线L于 B、C两点．
    （1）求证：∠ABC+∠ACB=90°；
    （2）当⊙O的半径R=5，BD=12时，求tan∠ABC的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．计算过程：$\sqrt{\frac{-20}{-5}}$=$\frac{\sqrt{-5×4}}{\sqrt{-5}}$=$\frac{\sqrt{-5}×\sqrt{4}}{\sqrt{-5}}$=$\sqrt{4}$=2正确吗？如果不正确，请改正．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．计算：（3$\sqrt{72}$-12$\sqrt{\frac{1}{2}}$+$\sqrt{32}$）÷2$\sqrt{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．计算：$\frac{1}{1+\sqrt{2}}+\frac{1}{\sqrt{2}+\sqrt{3}}+\frac{1}{\sqrt{3}+2}…+\frac{1}{\sqrt{n}+\sqrt{n+1}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．计算：$\sqrt{18}-\frac{2}{\sqrt{2}}$+$\sqrt{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．因式分解：
    （1）a2b2-a2-2ab-b2
    （2）x3-x2y+xy2-y3
    （3）（ax-by）2+（bx+ay）2
    （4）（x2-4y2）+（4y-1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．某餐厅中，一张桌子可以坐6人，如果把多张桌子摆在一起，可以有以下两种摆放方式．

    （1）当有5张桌子时，第一种摆放方式能坐22人，第二种摆放方式能坐14人，
    （2）当有n张桌子时，第一种摆放方式能坐4n+2人，第二种摆放方式能坐2n+4人，
    （3）一天中午餐厅要接待98位顾客共同就餐（即桌子要摆在一起），但餐厅只有25张这样的餐桌，若你是这个餐厅的经理，你打算选择哪种方式来摆放餐桌？为什么？

    查看答案和解析>>

    同步练习册答案