
 ��ֱ֪��y1=x+b��������y2=-x2+ax+c��һ������Ϊ��2��3������x=1Ϊ�������ߵĶԳ��ᣮ
��ֱ֪��y1=x+b��������y2=-x2+ax+c��һ������Ϊ��2��3������x=1Ϊ�������ߵĶԳ��ᣮ���� ��1���ѽ����������ֱ�߽���ʽ���b��ֵ��ȷ����ֱ�߽���ʽ���ѽ���������������߽���ʽ�õ�a��c�Ĺ�ϵʽ�������öԳ��ṫʽ���a��ֵ���������c��ֵ��ȷ���������߽���ʽ������������꼴�ɣ�
��2������������ͼ������ͼ���ҳ�ʹ��y1��y2��xȡֵ��Χ���ɣ�
��3����������ȷ����A��B���꣬���AB�ij�����ʾ��AB���ϵĸߣ�������ʾ��������ABP���������������ABP���С�ڵ���6���x�ķ�Χ���ɣ�
��� �⣺��1����ֱ��y1=x+b��������y2=-x2+ax+c��һ������Ϊ��2��3����
��ѽ��㣨2��3������y1=x+b���ã�3=2+b����b=1��
��ֱ�߽���ʽΪy1=x+1��
�ѽ������꣨2��3������������y2=-x2+ax+c�ã�-4+2a+c=3��
�ɶԳ���Ϊֱ��x=1���õ�-$\frac{a}{2����-1��}$=1����a=2��
��a=2����ã�c=3��
��������y2=-x2+2x+3��
�������߶�������Ϊ��1��4����
��2����y2=-x2+2x+3=0����ã�x1=3��x2=-1��
����������x�ύ������Ϊ��3��0���ͣ�-1��0����
��������ͼ����ͼ��ʾ��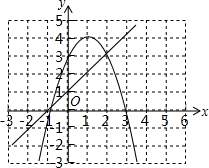
����ͼ��ɵ�ʹ��y1��y2��x��ΧΪ-1��x��2��
��3���ɣ�2���ɵ�A��3��0����
��x=3���õ�y1=3+1=4����B��3��4������AB=4��
��P������Ϊx��S��PAB�ĸ�Ϊ|3-x|����ΪAB=4��
��S��PAB��6���õ�$\frac{1}{2}$•|3-x|•4=2|3-x|��6��
��3-x��0����x��3ʱ������ʽ���εã�3-x��3��
��ã�x��0����ʱx��ΧΪ0��x��3��
��3-x��0����x��3ʱ������ʽ���εã�x-3��3��
��ã�x��6��
��ʱx�ķ�ΧΪ3��x��6��
���ϣ�x�ķ�ΧΪ0��x��6��
���� ���⿼���˴���ϵ��������κ�������ʽ�����κ����ϵ�������������������մ���ϵ�����ǽⱾ��Ĺؼ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ���Ʒ�� | A | B | C |
| ÿ���������أ��֣� | 10 | 8 | 6 |
| ÿ�������������Ԫ�� | 600 | 1000 | 800 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
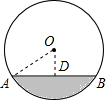 ��ͼ��С��֣����Ǧ���ڳ������ҳ�һ��С�ӣ�С�ӵ�ֱ��ABΪ10cm����Ϊ2cm��С�ӵ�������Ϊ2cm�������Ǧ��İ뾶OAΪ$\frac{29}{4}$cm��
��ͼ��С��֣����Ǧ���ڳ������ҳ�һ��С�ӣ�С�ӵ�ֱ��ABΪ10cm����Ϊ2cm��С�ӵ�������Ϊ2cm�������Ǧ��İ뾶OAΪ$\frac{29}{4}$cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
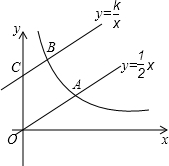 ��ͼ��ֱ��$y=\frac{1}{2}x$��˫����$y=\frac{k}{x}$��k��0��x��0�����ڵ�A����ֱ��$y=\frac{1}{2}x$����ƽ��4����λ���Ⱥ���y�ύ�ڵ�C����˫����$y=\frac{k}{x}$��k��0��x��0�����ڵ�B��
��ͼ��ֱ��$y=\frac{1}{2}x$��˫����$y=\frac{k}{x}$��k��0��x��0�����ڵ�A����ֱ��$y=\frac{1}{2}x$����ƽ��4����λ���Ⱥ���y�ύ�ڵ�C����˫����$y=\frac{k}{x}$��k��0��x��0�����ڵ�B���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
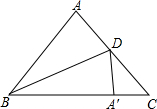 ��ͼ����ABC�У�AB=AC=5cm��BC=6cm��BDƽ�֡�ABC��BD��AC�ڵ�D���������ABD��BD���ۣ���A���ڵ�A�䴦����ô��DA��C�����Ϊ$\frac{12}{11}$cm2��
��ͼ����ABC�У�AB=AC=5cm��BC=6cm��BDƽ�֡�ABC��BD��AC�ڵ�D���������ABD��BD���ۣ���A���ڵ�A�䴦����ô��DA��C�����Ϊ$\frac{12}{11}$cm2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com