
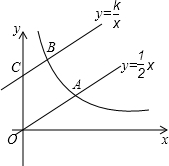
 如图,直线$y=\frac{1}{2}x$与双曲线$y=\frac{k}{x}$(k>0,x>0)交于点A,将直线$y=\frac{1}{2}x$向上平移4个单位长度后,与y轴交于点C,与双曲线$y=\frac{k}{x}$(k>0,x>0)交于点B.
如图,直线$y=\frac{1}{2}x$与双曲线$y=\frac{k}{x}$(k>0,x>0)交于点A,将直线$y=\frac{1}{2}x$向上平移4个单位长度后,与y轴交于点C,与双曲线$y=\frac{k}{x}$(k>0,x>0)交于点B.分析 (1)根据平移的性质得出平移后直线的解析式为y=$\frac{1}{2}$x+4,由点B在直线y=$\frac{1}{2}$x+4上,所以B(b,$\frac{1}{2}$b+4),点B在双曲线$y=\frac{k}{x}$(k>0,x>0)上,所以B(b,$\frac{k}{b}$),从而得出$\frac{1}{2}$b+4=$\frac{k}{b}$,整理即可求得;
(2)分别过点A、B作AD⊥x轴,BE⊥x轴,CF⊥BE于点F,再设设A(3x,$\frac{3}{2}$x),由于OA=3BC,故可得出B(x,$\frac{1}{2}$x+4),再根据反比例函数中k=xy为定值求出k的值即可.
解答 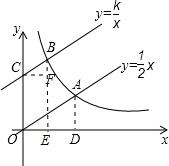 解:(1)∵将直线$y=\frac{1}{2}x$向上平移4个单位长度后,与y轴交于点C,
解:(1)∵将直线$y=\frac{1}{2}x$向上平移4个单位长度后,与y轴交于点C,
∴平移后直线的解析式为y=$\frac{1}{2}$x+4,
∵点B在直线y=$\frac{1}{2}$x+4上,
∴B(b,$\frac{1}{2}$b+4),
∵点B在双曲线$y=\frac{k}{x}$(k>0,x>0)上,
∴B(b,$\frac{k}{b}$),
∴$\frac{1}{2}$b+4=$\frac{k}{b}$,
∴k=$\frac{1}{2}$b2+4b;
(2)分别过点A、B作AD⊥x轴,BE⊥x轴,CF⊥BE于点F,设A(3x,$\frac{3}{2}$x),
∵OA=3BC,BC∥OA,CF∥x轴,
∴△BCF∽△AOD,
∴CF=$\frac{1}{3}$OD,
∵点B在直线y=$\frac{1}{2}$x+4上,
∴B(x,$\frac{1}{2}$x+4),
∵点A、B在双曲线$y=\frac{k}{x}$上,
∴3x•$\frac{3}{2}$x=x•($\frac{1}{2}$x+4),解得x=1,
∴k=3×1×$\frac{3}{2}$×1=$\frac{9}{2}$.
点评 本题考查的是反比例函数和一次函数的交点问题,平移的性质,函数图象上点的坐标特征,(2)根据题意作出辅助线,设出A、B两点的坐标,再根据k=xy的特点求出k的值即可.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图是每个面上都有一个汉字的正方体的一种侧面展开图,那么在原正方体的表面上,与汉字“美”相对的面上的汉字是( )
如图是每个面上都有一个汉字的正方体的一种侧面展开图,那么在原正方体的表面上,与汉字“美”相对的面上的汉字是( )| A. | 我 | B. | 爱 | C. | 丹 | D. | 东 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知直线y1=x+b与抛物线y2=-x2+ax+c的一个交点为(2,3),且x=1为该抛物线的对称轴.
已知直线y1=x+b与抛物线y2=-x2+ax+c的一个交点为(2,3),且x=1为该抛物线的对称轴.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
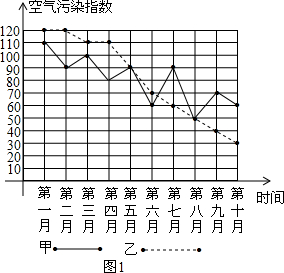 甲、乙两城市为了解决空气质量污染问题,对城市及其周边的环境污染进行了综合治理.在治理的过程中,环保部门每月初对两城市的空气质量进行监测,连续10个月的空气污染指数如图1所示.其中,空气污染指数≤50时,空气质量为优;50<空气污染指数≤100时,空气质量为良;100<空气污染指数≤150时,空气质量为轻微污染.
甲、乙两城市为了解决空气质量污染问题,对城市及其周边的环境污染进行了综合治理.在治理的过程中,环保部门每月初对两城市的空气质量进行监测,连续10个月的空气污染指数如图1所示.其中,空气污染指数≤50时,空气质量为优;50<空气污染指数≤100时,空气质量为良;100<空气污染指数≤150时,空气质量为轻微污染.| 平均数 | 方差 | 中位数 | 空气质量为优的次数 | |
| 甲 | 80 | 340 | 85 | 1 |
| 乙 | 80 | 1060 | 80 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com