
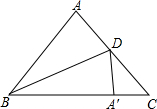
 如图,△ABC中,AB=AC=5cm,BC=6cm,BD平分∠ABC,BD交AC于点D,如果将△ABD沿BD翻折,点A落在点A′处,那么△DA′C的面积为$\frac{12}{11}$cm2.
如图,△ABC中,AB=AC=5cm,BC=6cm,BD平分∠ABC,BD交AC于点D,如果将△ABD沿BD翻折,点A落在点A′处,那么△DA′C的面积为$\frac{12}{11}$cm2. 分析 如图,作辅助线;首先运用勾股定理求出AE的长度,进而求出△ABC的面积;求出△DBA′、△CDA′的面积之比;证明△ABD、△A′BD的面积相等,即可解决问题.
解答 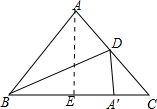 解:如图,过点A作AE⊥BC于点E;
解:如图,过点A作AE⊥BC于点E;
∵AB=AC,
∴BE=CE=3;由勾股定理得:
AB2=AE2+BE2,而AB=5,
∴AE=4,${S}_{△ABC}=\frac{1}{2}×6×4=12$;
由题意得:${S}_{△ABD}={S}_{△{A}^{′}BD}$,A′B=AB=5,
∴CA′=6-5=1,
∴$\frac{{S}_{△{A}^{′}BD}}{{S}_{△D{A}^{′}C}}=\frac{BA′}{C{A}^{′}}=\frac{5}{1}$,
∴若设${S}_{△D{A}^{′}C}=λ,则$${S}_{△ABD}={S}_{△{A}^{′}BD}$=5λ,
故λ+5λ+5λ=12,
∴λ=$\frac{12}{11}$(cm2),
故答案为$\frac{12}{11}$.
点评 该题主要考查了翻折变换的性质、等腰三角形的性质、勾股定理等几何知识点及其应用问题;解题的方法是作辅助线,构造直角三角形;解题的关键是灵活运用翻折变换的性质来分析、判断、解答.


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:解答题
 已知直线y1=x+b与抛物线y2=-x2+ax+c的一个交点为(2,3),且x=1为该抛物线的对称轴.
已知直线y1=x+b与抛物线y2=-x2+ax+c的一个交点为(2,3),且x=1为该抛物线的对称轴.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
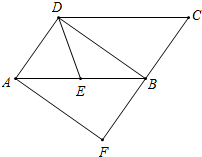 如图,在?ABCD中,E为边AB的中点,BD是对角线,AF∥DB交CB的延长线于F.若DE=BE,则四边形AFBD是什么特殊四边形?并证明你的结论.
如图,在?ABCD中,E为边AB的中点,BD是对角线,AF∥DB交CB的延长线于F.若DE=BE,则四边形AFBD是什么特殊四边形?并证明你的结论.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
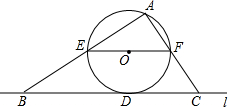 如图,直线L与⊙O相切于点D.过圆心O作EF∥L交⊙O于E、F两点,点A是⊙O上一点,连接AE、AF.并分别延长交直线L于 B、C两点.
如图,直线L与⊙O相切于点D.过圆心O作EF∥L交⊙O于E、F两点,点A是⊙O上一点,连接AE、AF.并分别延长交直线L于 B、C两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com