
(1)如图1,正方形ABCD中,点E,F分别在边BC,CD上,∠EAF=45°,延长
CD到点G,使DG=BE,连结EF,AG.求证:EF=FG.
(2)如图2,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点M,N在边
BC上,且∠MAN=45°,若BM=1,CN=3,求MN的长.
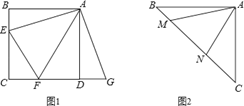

(1)证明:∵ABCD为正方形,
∴∠ABE=∠ADG,AD=AB,
在△ABE和△ADG中,
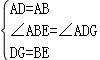
∴△ABE≌△ADG(SAS), 3分
∴∠BAE=∠DAG,AE =AG,
=AG,
∴∠EAG=90°,
在△FAE和△GAF中,
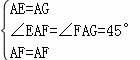 ,
,
∴△FAE≌△GAF(SAS),
∴EF=FG 6分
(2)解:如图2,过点C作CE⊥BC,垂足为点C,截取CE,使CE=BM.
连接AE、EN.

∵AB=AC,∠BAC=90°,∴∠B=∠ACN=45°.
∵CE⊥BC,∴∠ACE=∠B=45°.
在△ABM和△ACE中,
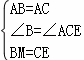
∴△ABM≌△ACE(SAS). 8分
∴AM=AE,∠BAM=∠CAE.
∵∠BAC=90°,∠MAN=45°,∴∠BAM+∠CAN=45°.
于是,由 ∠BAM=∠CAE,得∠MAN=∠EAN=45°.
∠BAM=∠CAE,得∠MAN=∠EAN=45°.
在△MAN和△EAN中,
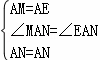
∴△MAN≌△EAN(SAS). 10分
∴MN=EN.
在Rt△ENC中,由勾股定理,得EN2=EC2+NC2.
∴MN2=BM2+NC2.
∵BM=1,CN=3,
∴MN2=12+32,
∴MN=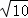 12分
12分


科目:初中数学 来源: 题型:
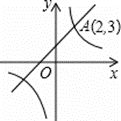
如图,一次函数y1=k1x+b(k1、b为常数,且k1≠0)的图象与反比例函数
y2=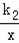 (k2为常数,且k2≠0)的图象都经过点A(2,3).则当x>2时,
(k2为常数,且k2≠0)的图象都经过点A(2,3).则当x>2时,
y1与y2的大小关系为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
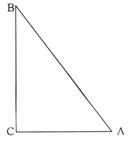
如图,Rt△ABC.中,∠C=90O。
(1) 用尺规作图作Rt△ABC的重心(三边中线的交点)P.(保留作图痕迹,不要求
写作法、证明);
(2) 你认为只要知道Rt△ABC哪一条边的长即可求出它的重心与外心(外接圆圆心)之间的距离?并请你说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
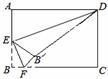
如图,在矩形ABCD中,AB=4,AD=6,E是AB边的中点,F是线段BC上的动点,
将△EBF沿EF所在直线折叠得到△EB′F,连接B′D,则B′D的小值是( )
A、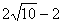 B、6 C、
B、6 C、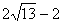 D、4
D、4
查看答案和解析>>
科目:初中数学 来源: 题型:
某小区为了绿化环境,计划分两次购进A、B两种花草,第一次分别购进A、B两种花草30棵和15棵,共花费675元;第二次分别购进A、B两种花草12棵和5棵.两次共花费940元(两次购进的A、B两种花草价格均分别相同).
(1)A、B两种花草每棵的价格分别是多少元?
(2)若购买A、B两种花草共31棵,且B种花草的数量少于A种花草的数量的2倍,请你给出一种费用最省的方案,并求出该方案所需费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com