
【题目】如图,在正方形![]() 中,
中,![]() 的顶点
的顶点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 边上,高
边上,高![]() 与正方形的边长相等,连接
与正方形的边长相等,连接![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,下列说法:①
,下列说法:①![]() ;②连接
;②连接![]() ,
,![]() ,则
,则![]() 为直角三角形;③
为直角三角形;③![]() ;④若
;④若![]() ,
,![]() ,则
,则![]() 的长为
的长为![]() ,其中正确结论的个数是( )
,其中正确结论的个数是( )
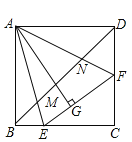
A.4B.3C.2D.1
【答案】A
【解析】
根据正方形的性质及HL定理求得Rt△AEB≌Rt△AEG,Rt△AFD≌Rt△AFG,从而求得∠EAB=∠EAG,∠FAD=∠FAG,然后求得2∠EAG+2∠FAG=90°,从而得到![]() ,由此判断①;
,由此判断①;
将△ADN绕点A顺时针旋转90°至△ABH位置,连接MH,MG,NG,由旋转的性质根据结合SAS定理求得△AHM≌△ANM,得到MN=MH,结合正方形和旋转的性质求得∠HBM=∠ABH+∠ABD=90°,从而可得MH2=HB2+BM2,然后根据SAS定理求得△ABM≌△AGM,△AND≌△AANG,从而得到BM=GM,DN=GN,从而求得MN2=MG2+NG2,由此判断②;
由垂直可得∠AEG =90°-∠EAG,然后结合①中已证∠EAG+∠FAG=∠EAG+∠FAD=45°,可得∠ANM=90°-∠EAG,由此得到∠AEG =∠ANM,然后根据AA定理求得三角形形式,由此判断③;
旋转△ABE到△ADH,由旋转性质和SAS定理可得得△ABE≌△ADH,△AEF≌△AHF,设CF=a,在Rt△CEF中,根据勾股定理列方程求a,从而求得正方形的边长,设MN=x,结合②中的结论列方程求x的值,从而判断④.
解:如图中,
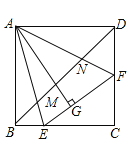
∵四边形ABCD是正方形,
∴AB=AD,∠ABC=∠ADC=90°,
∵AG⊥EF,
∴∠AGE=∠ABC=90°,
在Rt△AEB和Rt△AEG中,![]() ,
,
∴Rt△AEB≌Rt△AEG,
∴∠EAB=∠EAG,
同理可证Rt△AFD≌Rt△AFG,
∴∠FAD=∠FAG,
∴2∠EAG+2∠FAG=90°,
∴∠EAG+∠FAG=45°,
∴∠EAF=45°,故①正确;
如图②,将△ADN绕点A顺时针旋转90°至△ABH位置,连接MH,MG,NG
由旋转知:∠BAH=∠DAN,AH=AN,
∵四边形ABCD是正方形,
∴∠BAD=90°,
∵∠EAF=45°,
∴∠BAM+∠DAN=45°,
∴∠HAM=∠BAM+∠BAH=45°,
∴∠HAM=∠NAM,又AM=AM,
∴△AHM≌△ANM,
∴MN=MH
∵四边形ABCD是正方形,
∴∠ADB=∠ABD=45°.
由旋转知:∠ABH=∠ADB=45°,HB=ND,
∴∠HBM=∠ABH+∠ABD=90°,
∴MH2=HB2+BM2,
∴MN2=MB2+ND2.
又∵AB=AG,∠EAB=∠EAG,AM=AM
∴△ABM≌△AGM
∴BM=GM
同理可证:△AND≌△AANG
∴DN=GN
∴MN2=MG2+NG2
即![]() 为直角三角形,故②正确;
为直角三角形,故②正确;
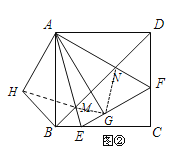
∵AG⊥EF
∴∠AEG =90°-∠EAG
又∵∠ANM=∠BDA+∠DAF=45°+∠DAF
由①可知:∠EAG+∠FAG=∠EAG+∠FAD=45°
∴∠ANM=90°-∠EAG
∴∠AEG =∠ANM
又∵![]()
∴![]() ,故③正确;
,故③正确;
如图3中,
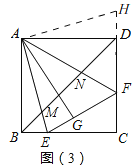
旋转△ABE到△ADH,△ABE≌△ADH
∴DH=BE=2,
同理②中可证:△AEF≌△AHF,
∴FH=EF,设CF=a
∴CD=CF+DF=a+3,EF=FH=DF+DH=5,
∵四边形ABCD是正方形,
∴BC=CD=a+3
∴CE=BC-BE=a+3-2=a+1,
在Rt△CEF中,根据勾股定理得,(a+1)2+32=25
∴a=3或a=-5(舍),
∴CF=3,
∴CD=6,
∴正方形的边长为6;
由正方形ABCD的边长为6,
∴BD=![]() CD=6
CD=6![]() ,
,

由①可知△MAN=45°,
∵AB=AD,∠BAD=90°,
由②得BM2+DN2=MN2,
设MN=x,
∵BD=6![]() ,BM=
,BM=![]() ,
,
∴DN=![]()
∴![]()
解得x=![]() ,
,
∴MN=![]() ,故④正确
,故④正确
故选:A.


科目:初中数学 来源: 题型:
【题目】阅读理解:给定一个矩形,如果存在另一个矩形,它的周长和面积分别是已知矩形的周长和面积的一半,则这个矩形是给定矩形的“减半”矩形.如图,矩形![]() 是矩形
是矩形![]() 的“减半”矩形.
的“减半”矩形.
请你解决下列问题:
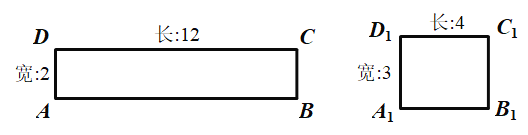
(1)当矩形的长和宽分别为![]() ,
,![]() 时,它是否存在“减半”矩形?请作出判断,并说明理由.
时,它是否存在“减半”矩形?请作出判断,并说明理由.
(2)边长为![]() 的正方形存在“减半”正方形吗?如果存在,求出“减半”正方形的边长;如果不存在,请说明理由.
的正方形存在“减半”正方形吗?如果存在,求出“减半”正方形的边长;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中装有4张卡片.4张卡片的正面分别标有数字1,2,3,4,这些卡片除数字外都相同,将卡片搅匀.
(1)从盒子任意抽取一张卡片,恰好抽到标有奇数卡片的概率是: ;
(2)先从盒子中任意抽取一张卡片,再从余下的3张卡片中任意抽取一张卡片,求抽取的2张卡片标有数字之和大于4的概率(请用画树状图或列表等方法求解).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了减少雾霾的侵状,某市环保局与市委各部门协商,要求市民在春节期间禁止燃放烟花爆竹,为了征集市民对禁燃的意见,政府办公室进行了抽样调查,调查意见表设计为:“满意““一般””无所谓””反对”四个选项,调查结果汇总制成如下不完整的统计图,请根据提供的信息解答下面的问题.
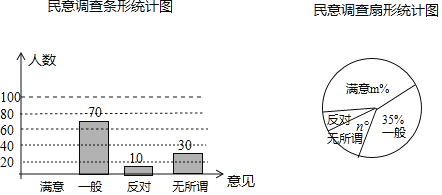
(1)参与问卷调查的人数为 .
(2)扇形统计图中的m= ,n= .补全条形统计图;
(3)若本市春节期间留守市区的市民有32000人,请你估计他们中持“反对”意见的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店准备购进![]() 两种商品,
两种商品,![]() 种商品毎件的进价比
种商品毎件的进价比![]() 种商品每件的进价多20元,用3000元购进
种商品每件的进价多20元,用3000元购进![]() 种商品和用1800元购进
种商品和用1800元购进![]() 种商品的数量相同.商店将
种商品的数量相同.商店将![]() 种商品每件的售价定为80元,
种商品每件的售价定为80元,![]() 种商品每件的售价定为45元.
种商品每件的售价定为45元.
(1)![]() 种商品每件的进价和
种商品每件的进价和![]() 种商品每件的进价各是多少元?
种商品每件的进价各是多少元?
(2)商店计划用不超过1560元的资金购进![]() 两种商品共40件,其中
两种商品共40件,其中![]() 种商品的数量不低于
种商品的数量不低于![]() 种商品数量的一半,该商店有几种进货方案?
种商品数量的一半,该商店有几种进货方案?
(3)端午节期间,商店开展优惠促销活动,决定对每件![]() 种商品售价优惠
种商品售价优惠![]() (
(![]() )元,
)元,![]() 种商品售价不变,在(2)条件下,请设计出销售这40件商品获得总利润最大的进货方案.
种商品售价不变,在(2)条件下,请设计出销售这40件商品获得总利润最大的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
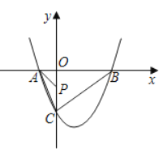
【题目】如图,已知二次函数![]() 的图象交
的图象交![]() 轴于
轴于![]() ,
,![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,其中
,其中![]() .
.
(1)求点![]() 的坐标,并用含
的坐标,并用含![]() 的式子表示
的式子表示![]() ;
;
(2)连接![]() ,
,![]() ,当
,当![]() 为锐角时,求
为锐角时,求![]() 的取值范围;
的取值范围;
(3)若![]() 为
为![]() 轴上一个动点,连接
轴上一个动点,连接![]() ,当点
,当点![]() 的坐标为
的坐标为![]() 时,直接写出
时,直接写出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学疫情期间为了切实抓好“停课不停学”活动,借助某软件平台随机抽取了该校部分学生的在线学习时间,并将结果绘制成如下两幅不完整的统计图.

请你根据以上信息回答下列问题
(1)本次调查的人数为 , 学习时间为7小时的所对的圆心角为 ;
(2)补全频数分布直方图;
(3)若全校共有学生1800人,估计有多少学生在线学习时间不低于8个小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校数学社团的同学们在学生中开展“了解校训意义”的调查活动.采取随机抽样的方式进行问卷调查.问卷调查的结果分为![]() 、
、![]() 、
、![]() 、
、![]() 四类.
四类.![]() 类表示非常了解;
类表示非常了解;![]() 类表示比较了解;
类表示比较了解;![]() 类表示基本了解;
类表示基本了解;![]() 类表示不太了解.(要求每位同学必须选并且只能选择一项)统计数据整理如表:
类表示不太了解.(要求每位同学必须选并且只能选择一项)统计数据整理如表:
类别 | 频数 | 频率 |
| 20 |
|
|
| 0.3 |
| 11 | 0.22 |
| 4 | 0.08 |
(1)表中![]() __________;
__________;![]()
(2)根据表中数据,求出![]() 类同学数所对应的扇形圆心角为_________度.
类同学数所对应的扇形圆心角为_________度.
(3)根据调查结果,请你估计该校1500名学生中对校训“非常了解”的人数;
(4)学校在开展了解校训意义活动中,需要从![]() 类的甲、乙、丙、丁四名同学中随机选取2人参加展示活动,求恰好选中甲乙两人的概率?(请用列表法或是树状图表示)
类的甲、乙、丙、丁四名同学中随机选取2人参加展示活动,求恰好选中甲乙两人的概率?(请用列表法或是树状图表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菱形ABCD中,AE⊥BC于E,交BD于F点,下列结论:
①BF为∠ABE的角平分线;
②DF=2BF;
③2AB2=DFDB;
④sin∠BAE=![]() .其中正确的为( )
.其中正确的为( )
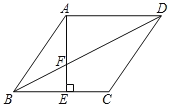
A.①③B.①②④C.①④D.①③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com