考点:解一元二次方程-因式分解法,解一元二次方程-直接开平方法,解一元二次方程-配方法,解一元二次方程-公式法
专题:
分析:(1)先找出a,b,c,再求出判别式,用公式法解即可;
(2)用十字相乘法求解即可;
(3)提公因式,再得出两个一元一次方程,求解即可;
(4)先找出a,b,c,再求出判别式,用公式法解即可;
(5)提公因式,再得出两个一元一次方程,求解即可;
(6)去括号,整理成一元二次方程的一般形式,用因式分解法求解即可.
解答:解:(1)a=2,b=-4,c=1,
△=b
2-4ac=16-8=8>0,
方程有两个不相等的实数根,
x=
=
=
,
x
1=
,x
2=
;
(2)(x-6)(x+1)=0,
x-6=0或x+1=0,
x
1=6,x
2=-1;
(3)2(x-3)
2=x(x-3),
2(x-3)
2-x(x-3)=0
(x-3)(2x-6-x)=0,
x-3=0或x-6=0,
x
1=3,x
2=6;
(4)a=1,b=-2
,c=1,
△=b
2-4ac=20-4=16>0,
方程有两个不相等的实数根,
x=
=
=
±2,
x
1=
+2,x
2=
-2;
(5)a=2,b=5,c=-3,
△=b
2-4ac=25+24=49>0,
方程有两个不相等的实数根,
x=
=
,
x
1=
,x
2=-3;
(6)9-6x+x
2+x
2=9,
2x
2-6x=0,
2x(x-3)=0
2x=0或x-3=0,
解得x
1=0,x
2=3.
点评:本题考查了用因式分解法解一元二次方程,解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.



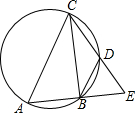 如图,已知△ABC内接于⊙O,D是
如图,已知△ABC内接于⊙O,D是
