
����Ŀ����ƽ��ֱ������ϵxOy�У�ֱ��y��kx+b��k��0����������y��ax2��4ax+3a�ĶԳ��ύ�ڵ�A��m����1������A����x��ĶԳƵ�ǡΪ�����ߵĶ��㣮
��1���������ߵĶԳ��ἰa��ֵ��
��2���ᡢ�����궼�������ĵ�������㣮��ֱ��y��kx+b��k��0����������Χ�ɵķ���������߽磩ΪW��
����k��1ʱ��ֱ��д������W�ڵ����������
��������W��ǡ��3�����㣬��Ϻ���ͼ����b��ȡֵ��Χ��
���𰸡���1��![]() ��
��![]() ����2����2����
����2����2����![]() ��
��![]() .
.
��������
��1��������![]() ����Ϊ����ʽ����Գ���x=2�붥�����꣨2,1�������뼴����a����2����ͼ��ʾ���ٵ�
����Ϊ����ʽ����Գ���x=2�붥�����꣨2,1�������뼴����a����2����ͼ��ʾ���ٵ�![]() ʱ������
ʱ������![]() �ڵ��������Ϊ2������
�ڵ��������Ϊ2������![]() ����ֱ�߹�
����ֱ�߹�![]() ��
��![]() �������
�������![]() ��
��![]() ���ֱ������bֵ���������ȡֵ��Χ����
���ֱ������bֵ���������ȡֵ��Χ����![]() ���ɶԳ��Կɵ�b��ȡֵ��Χ.
���ɶԳ��Կɵ�b��ȡֵ��Χ.
��![]() ��ȡֵ��Χ�ǣ�
��ȡֵ��Χ�ǣ�![]() ��
��![]() ��
��
�⣺��1�����εã�![]() .
.
��Գ���Ϊ![]() ��
��
���![]() ������Ϊ
������Ϊ![]() �ɵ������߶���Ϊ
�ɵ������߶���Ϊ![]()
�ѵ�![]() ������������߿ɵã�
������������߿ɵã�![]() ��
��

��2���ٵ�![]() ʱ������
ʱ������![]() �ڵ��������Ϊ2����
�ڵ��������Ϊ2����
����![]() ��
��
��ֱ�߹�![]() ��
��![]() ʱ��
ʱ��![]() ��
��
��ֱ�߹�![]() ��
��![]() ʱ��
ʱ��![]() ��
��
��![]() ��
��
��![]() ��
��
�ɶԳ��Կɵã�![]() ��
��
��![]() ��ȡֵ��Χ�ǣ�
��ȡֵ��Χ�ǣ�![]() ��
��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
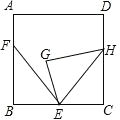
����Ŀ����ͼ�������� ABCD �У��� E��F �ֱ��� BC �� AB �ϣ�BE��3��AF��2��BF��4������ BEF �Ƶ� E ˳ʱ����ת���õ���GEH������ H ���� CD ����ʱ��F��H ����֮��ľ���Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������x�ķ���mx2��x��m+1��0���������������ۣ�
�ٵ�m��0ʱ������ֻ��һ��ʵ���⣻
�ڵ�m��0ʱ����������������ȵ�ʵ���⣻
������mȡ��ֵ�����̶���һ����������
(1)�����жϣ���������������ȷ����_____(�����)
(2)֤��(1)������Ϊ��ȷ�Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
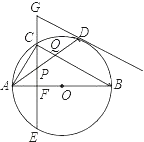
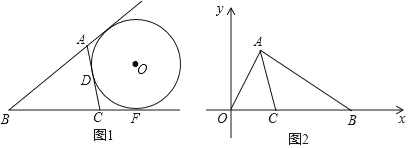
����Ŀ����ͼ���ڡ�O�У�AB��ֱ������D�ǡ�O��һ�㣬��C��![]() ���е㣬��CE��AB�ڵ�F������D�����߽�EC���ӳ����ڵ�G������AD���ֱ�CF��BC�ڵ�P��Q������AC���������н��ۣ��١�BAD����ABC����GP��GD���۵�P�ǡ�ACQ�����ģ���APAD��CQCB��������ȷ����_____��д��������ȷ���۵���ţ���
���е㣬��CE��AB�ڵ�F������D�����߽�EC���ӳ����ڵ�G������AD���ֱ�CF��BC�ڵ�P��Q������AC���������н��ۣ��١�BAD����ABC����GP��GD���۵�P�ǡ�ACQ�����ģ���APAD��CQCB��������ȷ����_____��д��������ȷ���۵���ţ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���y��x2��2x��3��ͼ����x�ύ��A��B���㣬��y�ύ�ڵ�C��������˵��������ǣ�������
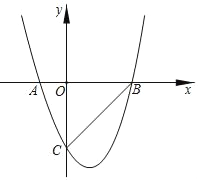
A. AB��4
B. ��ABC��45��
C. ��x��0ʱ��y����3
D. ��x��1ʱ��y��x�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
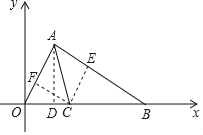
����Ŀ����ͼ��ijͬѧ��һ����ҵ��Ľ���˼·��������ʦ���ݴ�չ�������ۣ�������ͼ����֪A��1��![]() ����B��4��0������OAB��ƽ����AC��x���ڵ�C����OC�ij���˼·����AD��OB��CE��AB��CF��OA
����B��4��0������OAB��ƽ����AC��x���ڵ�C����OC�ij���˼·����AD��OB��CE��AB��CF��OA
��A�����OD��1��AD��![]() ��OA��2����AOC��60�㣻
��OA��2����AOC��60�㣻
��A��B�����OA��2��OB��4��AB��2![]() ����OAB��90�㣻
����OAB��90�㣻
��ACƽ�֡�OAB��CE��CF��
��S��AOC+S��ABC��S��AOB��AOCF+ABCE��OAAB��CF��3��![]() ��
��
�����ϣ�Rt��OCF�У�OC��![]() ��2�������Ż���
��2�������Ż���
��1��ͬѧ�Ƿ��ֲ���Ҫ֤����OAB��90�㡱Ҳ����⣬��Ҫ˵�����ɣ���λͬѧ����˲�ͬ��˼·
�ټ�˵��S��AOC��S��ABC�����֮�ȼ���![]() ������
������![]() ���Ӷ�
���Ӷ�![]() ��
��
����˵����AB����ȡ��G��ʹAG��AO������CG����֪BG�ij���Ϊ����
�۱�˵���ӳ�AC����AOB�����Բ��N��������һ�κ������������OC��
����ѡ������һ�ֽⷨ������ͼ2�����в�����ɽ����ʲô�ջ�
��2���������ͼ��������ȷ��������ϵ����Ч�������������������⣺��ͼ1����O���ABC�ı�AC����BA��BC���ӳ���AE��CF���У��е�ֱ�ΪD��E��F�����ABC�����ΪS��BC��a��AC��b��AB��c�����ú�S��a��b��c��ʽ�ӱ�ʾ��O�İ뾶R��ֱ��д�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���B=90�㣬AB=12��BC=24������P�ӵ�A��ʼ�ر�AB���յ�B��ÿ��2����λ���ȵ��ٶ��ƶ�������Q�ӵ�B��ʼ�ر�BC��ÿ��4����λ���ȵ��ٶ����յ�C�ƶ��������P��Q�ֱ�ӵ�A��Bͬʱ��������ô��PBQ�����S�����ʱ��t��s����α仯��д��������ϵʽ��t��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
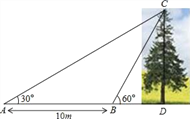
����Ŀ����ͼ��ij��ѧ��ȤС�������һ����CD�ĸ߶ȣ��������ڵ�A���������C������Ϊ30�㣬Ȼ����AD����ǰ��10m������B�㣬��B���������C�����Ǹ߶�Ϊ60�㣨A��B��D������ͬһֱ���ϣ�������������Dz������ݼ��������CD�ĸ߶ȣ������ȷ��0.1m�������ο����ݣ�![]() ��1.414��
��1.414��![]() ��1.732��
��1.732��
���𰸡�8.7��
������������������������������ε���ǵ����������ACB�Ķ������õ�BC�ij��ȣ�Ȼ����ֱ����BDC�У��������Ǻ���������⣮
����������ߡ�CBD=��A+��ACB��
���ACB=��CBD����A=60�㩁30��=30����
���A=��ACB��
��BC=AB=10���ף���
��ֱ����BCD�У�CD=BCsin��CBD=10��![]() =5
=5![]() ��5��1.732=8.7���ף���
��5��1.732=8.7���ף���
�������CD�ĸ߶�Ϊ8.7�ף�
���㣺��ֱ�������ε�Ӧ��
�����͡������
��������
23
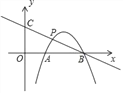
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y=��x2+ax+b��x����A��1��0����B��3��0�����㣬��P�����������ڵ�һ�����ڵ�һ�㣬ֱ��BP��y���ཻ�ڵ�C��
��1����������y=��x2+ax+b�Ľ���ʽ��
��2������P���߶�BC���е�ʱ�����P�����ꣻ
��3���ڣ�2���������£���sin��OCB��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
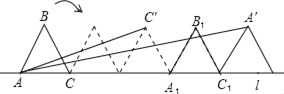
����Ŀ����ͼ����֪�߳�Ϊ2����������ABC����ֱ��l������
(1)����ABC����һ�ܵ���A1B1C1��λ�ã���ʱA���˶���·��Ϊ�� ����ԼΪ������(��ȷ��0.1������3.14��)
(2)���ABC����240��ʱ��C���λ��ΪC�䣬��ABC����480��ʱ��A���λ��ΪA�䣮�����������Ǻ��������е����Ǻ�ʽtan(��+��)��(tan��+tan��)��(1��tan��tan��)�������CAC��+��CAA��Ķ�����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com