
在直角坐标系中,以原点为圆心,4为半径作圆,该圆上到直线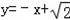
 的距离等于2的点共有( )
的距离等于2的点共有( )
A.1个 B.2个 C.3个 D.4个
D【考点】垂径定理;坐标与图形性质;三角形内角和定理;勾股定理;直线与圆的位置关系.
【专题】计算题.
【分析】过O作OH⊥AB,求出O到直线的距离,和圆的半径比较得出圆于直线相交,且圆心到直线的距离是1,画出图形,得出在直线的两旁到直线的距离等于2的点有4个点,即可得出答案.
【解答】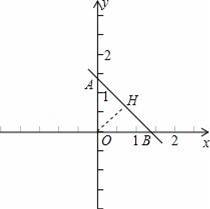

解:过O作OH⊥AB于H,
y=﹣x+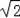
 ,
,
∵当x=0时,y=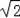
 ,
,
当y=0时,x=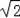
 ,
,
∴AO=OB=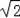
 ,
,
由勾股定理得:AB=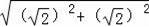
 =2,
=2,
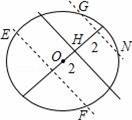
由三角形的面积公式得:AB×OH=AO×OB,
即2OH=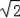
 ×
×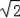
 =2,
=2,
解得:OH=1<4,
即直线与圆相交,
如图:
在直线的两旁到直线的距离等于2的点有4个点(E、F、G、N),
故选D.

【点评】本题考查了直线与圆的位置关系和三角形的面积的应用,关键是求出直线与圆的位置关系和画出第二个图形,主要考查学生的理解能力和推理能力,题目有一定的难度,注意:不要漏解啊.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
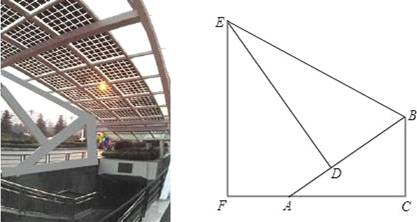
如图是某地下商业街的入口,数学课外兴趣小组的同学打算运用所学的知识测量侧面支架的最高点E到地面的距离EF.经测量,支架的立柱BC与地面垂直,即∠BCA=90°,且BC=1.5m,点F、A、C在同一条水平线上,斜杆AB与水平线AC的夹角∠BAC=30°,支撑杆DE⊥AB于点D,该支架的边BE与AB的夹角∠EBD=60°,又测得AD=1m.请你求出该支架的边BE及顶端E到地面的距离EF的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
一个口袋中装有10个红球和若干个黄球,在不允许将求倒出来数的前提下,为估计袋中黄球的个数,小明采用了如下的方法:每次先从口袋中摸出10个球,求出其中红球数与10的比值,再把球放回口袋中摇匀,不断重复上述过程20次,得到红球与10的比值的平均数为0.4,根据上述数据,估计口袋中大约有( )个黄球.
A.30 B.15 C.20 D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
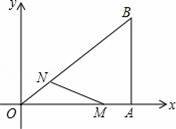
如图,在直角坐标系中,Rt△OAB的直角顶点A在x轴上,OA=4,AB=3.动点M从点A出发,以每秒1个单位长度的速度,沿AO向终点O移动;同时点N从点O出发,以每秒1.25个单位长度的速度,沿OB向终点B移动.当两个动点运动了x秒(0<x<4)时,解答下列问题:
(1)求点N的坐标(用含x的代数式表示);
(2)设△OMN的面积是S,求S与x之间的函数表达式;当x为何值时,S有最大值?最大值是多少?
(3)在两个动点运动过程中,是否存在某一时刻,使△OMN是直角三角形?若存在,求出x的值;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com