练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

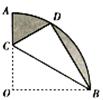
    如图，在扇形OAB中，∠AOB=90°，半径OA=2．将扇形OAB沿过点B的直线折叠．点O恰好落在弧AB上点D处，折痕交OA于点C，则图中阴影部分的面积为     ．

     


        

     
     



      ；      

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    已知：∠MAN=60°，点B在射线AM上，AB=4（如图）．P为直线AN上一动点，以BP为边作等边三角形BPQ（点B，P，Q按顺时针排列），O是△BPQ的外心．

    （1）当点P在射线AN上运动时，求证：点O在∠MAN的平分线上；

    （2）当点P在射线AN上运动（点P与点A不重合）时，AO与BP交于点C，设AP=x，AC•AO=y，求y关于x的函数解析式，并写出函数的定义域；

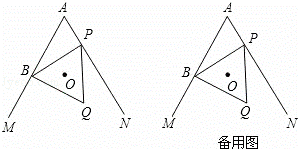    （3）若点D在射线AN上，AD=2，圆I为△ABD的内切圆．当△BPQ的边BP或BQ与圆I相切时，请直接写出点A与点O的距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    观察下列各式，找规律：

    ①32﹣12=4×2；

    ②42﹣22=4×3；

    ③52﹣32=4×4；

    ④62﹣42=4×5，

    第n个等式是　　　　　　．（n是正整数）

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    二次函数的顶点坐标是   （  ）

      A．(－1，2)    B．(1，2)        C．(2，1)      D．(－1，－2)

    查看答案和解析>>

    科目：初中数学 来源： 题型：


     已知二次函数y=x2-8x+m的最小值为1，那么m的值为      .

    查看答案和解析>>

    科目：初中数学 来源： 题型：


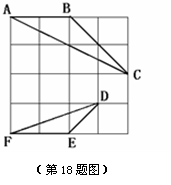
    在4×4的正方形方格中，△ABC和△DEF的顶点都在边长为1的小正方形的顶点上．

    （1）判断△ABC与△DEF是否相似，并说明理由．

    （2）请在图中再画一个和△ABC相似，但与图中三角形均不全等的格点三角形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图：已知△ABC中，AB＝5，BC＝3，AC＝4，PQ∥AB，P点在AC上(与A、C不重合)，Q在BC上．

    (1) 当△PQC的面积等于四边形PABQ面积的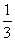，求CP的长．

    (2)当△PQC的周长与四边形PABQ的周长相等时，求CP的长．

    (3)试问：在AB上是否存在一点M，使得△PQM为等腰直角三角形，若不存在，请简要说明理由：若存在，请求出PQ的长．

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    △ABC中，∠A、∠B都是锐角，若sinA＝，cosB＝，则∠C＝　    　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    .单项式的次数是（    ）

    　A．6        B．5          C．3          D．2

    查看答案和解析>>

    同步练习册答案