
观察下列各式,找规律:
①32﹣12=4×2;
②42﹣22=4×3;
③52﹣32=4×4;
④62﹣42=4×5,
第n个等式是 .(n是正整数)
科目:初中数学 来源: 题型:
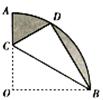
如图,在扇形OAB中,∠AOB=90°,半径OA=2.将扇形OAB沿过点B的直线折叠.点O恰好落在弧AB上点D处,折痕交OA于点C,则图中阴影部分的面积为 .
 |
| |
查看答案和解析>>
科目:初中数学 来源: 题型:
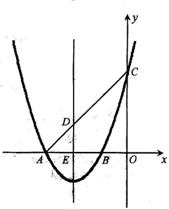
如图,已知抛物线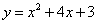 交x轴于A、B两点,交y轴于点C,抛物线的对称轴交x轴于点E,点B的坐标为(-1,0)。
交x轴于A、B两点,交y轴于点C,抛物线的对称轴交x轴于点E,点B的坐标为(-1,0)。
(1)求抛物线的对称轴及点A的坐标;
(2)在平面直角坐标系xoy中是否存在点P ,与A、B、C三点构成一个平行四边形?若存在,请写出点P的坐标;若不存在,请说明理由;
,与A、B、C三点构成一个平行四边形?若存在,请写出点P的坐标;若不存在,请说明理由;
(3)连结CA与抛物线的对称轴交于点D,在抛物线上是否存在点M,使得直线CM把四边形DEOC分成面积相等的两部分?如果存在,请求出点M的坐标,如果不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com