
已知:∠MAN=60°,点B在射线AM上,AB=4(如图).P为直线AN上一动点,以BP为边作等边三角形BPQ(点B,P,Q按顺时针排列),O是△BPQ的外心.
(1)当点P在射线AN上运动时,求证:点O在∠MAN的平分线上;
(2)当点P在射线AN上运动(点P与点A不重合)时,AO与BP交于点C,设AP=x,AC•AO=y,求y关于x的函数解析式,并写出函数的定义域;
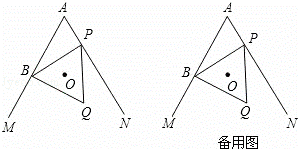 (3)若点D在射线AN上,AD=2,圆I为△ABD的内切圆.当△BPQ的边BP或BQ与圆I相切时,请直接写出点A与点O的距离.
(3)若点D在射线AN上,AD=2,圆I为△ABD的内切圆.当△BPQ的边BP或BQ与圆I相切时,请直接写出点A与点O的距离.
 (1)证明:如图1,连接OB,OP.
(1)证明:如图1,连接OB,OP.
∵O是等边三角形BPQ的外心,
∴圆心角∠BOP=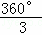 =120°.
=120°.
当∠MAN=60°,不垂直于AM时,作OT⊥AN,则OB=OP.
由∠HOT+∠A+∠AHO+∠ATO=360°,且∠A=60°,∠AHO=∠ATO=90°,
∴∠HOT=120度.
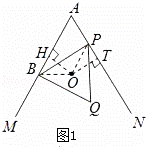 ∴∠BOH=∠POT.
∴∠BOH=∠POT.
∴Rt△BOH≌Rt△POT.
∴OH=OT.
∴点O在∠MAN的平分线上.
当OB⊥AM时,∠APO=360°﹣∠A﹣∠BOP﹣∠OBA=90°.
即OP⊥AN,
∴点O在圆I的平分线上.
综上所述,当点P在射线AN上运动时,点O在∠MAN的平分线上.
(2)解:如图2,
∵AO平分∠MAN,且∠MAN=60°,
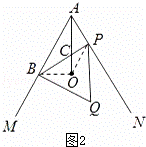 ∴∠BAO=∠PAO=30°.
∴∠BAO=∠PAO=30°.
由(1)知,OB=OP,∠BOP=120°,
∴∠CBO=30°,
∴∠CBO=∠PAC.
∵∠BCO=∠PCA,
∴∠AOB=∠APC.
∴△ABO∽△ACP.
∴ .
.
∴AC•AO=AB•AP.
∴y=4x.
定义域为:x>0.
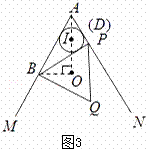
(3)解:①如图3,当BP与圆I相切时,AO=2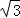 ;
;
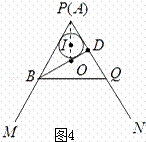
②如图4,当BP与圆I相切时,AO=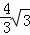 ;
;
③如图5,当BQ与圆I相切时,AO=0.



科目:初中数学 来源: 题型:
如图,在△ABC中,∠C=90°,D是AC上一点,DE⊥AB于点E,若AC=8,BC=6,DE=3,则AD的长为  ( )
( )
A. 3 B. 4 C. 5 D. 6
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
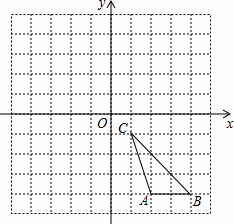
如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系内,△ABC的三个顶点坐标分别为A(2,﹣4),B(4,﹣4),C(1,﹣1).
(1)画出△ABC关于y轴对称的△A1B1C1,直接写出点A1的坐标 ;
(2)画出△ABC绕点O逆时针旋转90°后的△A2B2C2;
(3)在(2)的条件下,求线段BC扫过的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
下列适合普查的是( )
A.了解一批圆珠笔芯的使用寿命
B.了解我国2015~2016学年度七年级学生的视力情况
C.了解全班同学的年龄
D.鞋厂检验生产的鞋底能承受的弯折次数
查看答案和解析>>
科目:初中数学 来源: 题型:
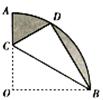
如图,在扇形OAB中,∠AOB=90°,半径OA=2.将扇形OAB沿过点B的直线折叠.点O恰好落在弧AB上点D处,折痕交OA于点C,则图中阴影部分的面积为 .
 |
| |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com