
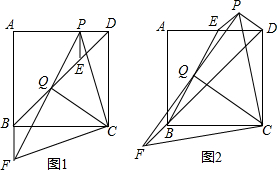
分析 (1)①证明△PDE是等腰直角三角形,得出PD=PE,证出∠BFQ=∠EPQ,由旋转的性质得:BF=PD=PE,由AAS证明△BFQ≌△EPQ,即可得出结论;
②由①得:△BFQ≌△EPQ,由全等三角形的性质得出FQ=PQ=$\frac{1}{2}$PF由旋转的性质得:CF=CP,∠PCF=90°,由等腰直角三角形的性质得出CQ=$\frac{1}{2}$PF,CQ⊥PF,即可得出结论;
(2)由旋转的性质得:PD=BF=PE,延长CB至G,则∠GBF=∠CBD=45°=∠PED,证出∠FBQ=∠PEQ,由AAS证明△FBQ≌△PEQ,得出FQ=PQ=$\frac{1}{2}$PF,证出∠FCP=∠BCD=90°,由等腰直角三角形的性质得出CQ=$\frac{1}{2}$PF,CQ⊥PF,即可得出结论;
(3)理由同(2).
解答 (1)①证明:∵四边形ABCD是正方形,
∴∠PDE=45°,AB⊥AD,∠BCD=90°,AD∥BC,
∵PE⊥AD,
∴△PDE是等腰直角三角形,AF∥PE,
∴PD=PE,∠BFQ=∠EPQ,
由旋转的性质得:BF=PD=PE,
在△BFQ和△EPQ中,$\left\{\begin{array}{l}{∠BFQ=∠EPQ}&{\;}\\{∠BQF=∠EQP}&{\;}\\{BP=EP}&{\;}\end{array}\right.$,
∴△BFQ≌△EPQ(AAS),
∴BQ=EQ;
②解:PQ=CQ,PQ⊥CQ;理由如下:
由①得:△BFQ≌△EPQ,
∴FQ=PQ=$\frac{1}{2}$PF,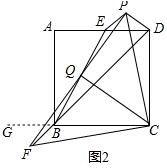
由旋转的性质得:CF=CP,∠PCF=90°,
∴CQ=$\frac{1}{2}$PF,CQ⊥PF,
∴PQ=CQ,PQ⊥CQ;
(2)解:结论PQ=CQ,PQ⊥CQ仍然成立;理由如下:
由旋转的性质得:PD=BF=PE,
延长CB至G,如图2所示:
则∠GBF=∠CBD=45°=∠PED,
∵AD∥BC,∴∠DEQ=∠GBQ,
∴∠FBQ=∠PEQ,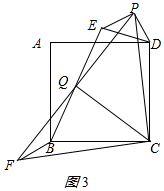
在△FBQ和△PEQ中,$\left\{\begin{array}{l}{∠FQB=∠PQE}&{\;}\\{∠FBQ=∠PEQ}&{\;}\\{BF=PE}&{\;}\end{array}\right.$,
∴△FBQ≌△PEQ(AAS),
∴FQ=PQ=$\frac{1}{2}$PF,
又∵∠FCB=∠PCD,
∴∠FCP=∠BCD=90°,
∵CF=CP,
∴CQ=$\frac{1}{2}$PF,CQ⊥PF,
∴PQ=CQ,PQ⊥CQ;
(3)解:结论PQ=CQ,PQ⊥CQ成立;如图3所示:
理由同(2).
点评 本题是四边形综合题目,考查了正方形的性质、旋转的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质、平行线的性质等知识;本题综合性强,有一定难度,证明三角形全等是解决问题的关键.


科目:初中数学 来源: 题型:解答题
| 每月每户用水量 | 每吨价(元) |
| 不超过10吨部分 | 0.50 |
| 超过10吨而不超过20吨部分 | 0.75 |
| 超过20吨部分 | 1.50 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ③④ | C. | ①②③ | D. | ①②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| a/m | … | $\frac{1}{2}$ | 1 | $\frac{3}{2}$ | 2 | $\frac{5}{2}$ | 3 | … |
| cm 2 | … | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 10 | B. | 6 | C. | -10 | D. | -6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{\frac{1}{4}}$ | B. | $\sqrt{(-2)^{2}}$ | C. | -$\sqrt{2}$ | D. | $\sqrt{-\frac{1}{4}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com