
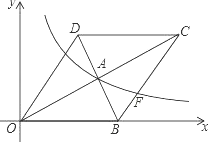
【题目】如图,在平面直角坐标系中,菱形OBCD的边OB在x轴正半轴上,反比例函数y=![]() (x>0)的图象经过该菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(6,8),则点F的坐标是 .
(x>0)的图象经过该菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(6,8),则点F的坐标是 .
【答案】(12,![]() ).
).
【解析】
首先过点D作DM⊥x轴于点M,过点F作FE⊥x于点E,由点D的坐标为(6,8),可求得菱形OBCD的边长,又由点A是BD的中点,求得点A的坐标,利用待定系数法即可求得反比例函数y=![]() (x>0)的解析式,然后由tan∠FBE=tan∠DOM=
(x>0)的解析式,然后由tan∠FBE=tan∠DOM=![]() ,可设EF=4a,BE=3a,则点F的坐标为:(10+3a,4a),即可得方程4a(10+3a)=32,继而求得a的值,则可求得答案.
,可设EF=4a,BE=3a,则点F的坐标为:(10+3a,4a),即可得方程4a(10+3a)=32,继而求得a的值,则可求得答案.
试题过点D作DM⊥x轴于点M,过点F作FE⊥x于点E,
∵点D的坐标为(6,8),
∴OD=![]() =10,
=10,
∵四边形OBCD是菱形,
∴OB=OD=10,
∴点B的坐标为:(10,0),
∵AB=AD,即A是BD的中点,
∴点A的坐标为:(8,4),
∵点A在反比例函数y=![]() 上,
上,
∴k=xy=8×4=32,
∵OD∥BC,
∴∠DOM=∠FBE,
∴tan∠FBE=tan∠DOM=![]() ,
,
设EF=4a,BE=3a,
则点F的坐标为:(10+3a,4a),
∵点F在反比例函数y=![]() 上,
上,
∴4a(10+3a)=32,
即3a2+10a﹣8=0,
解得:a1=![]() ,a2=﹣4(舍去),
,a2=﹣4(舍去),
∴点F的坐标为:(12,![]() ).
).
故答案为(12,![]() ).
).


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
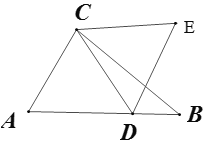
【题目】如图,△ABC中,AB=8,AC=5,BC=7,点D在AB上一动点,线段CD绕点C逆时针旋转60°得到线段CE,AE的最小值为________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国青少年发展基金会为某地“希望小学”捐赠物资,其中文具和食品共320件,文具比食品多80件.
(1)求文具和食品各多少件;
(2)现计划租用甲、乙两种货车共8辆,一次性将这批文具和食品全部运往该地.已知甲种货车最多可装文具40件和食品10件,乙种货车最多可装文具和食品各20件.则中国青少年发展基金会安排甲、乙两种货车时有几种方案?请你帮助设计出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校数学兴趣小组的同学测量一架无人飞机P的高度,如图,A,B两个观测点相距![]() ,在A处测得P在北偏东71°方向上,同时在B处测得P在北偏东35°方向上.求无人飞机P离地面的高度.(结果精确到1米,参考数据:
,在A处测得P在北偏东71°方向上,同时在B处测得P在北偏东35°方向上.求无人飞机P离地面的高度.(结果精确到1米,参考数据:![]() ,
,![]() ,sin71°≈0.95,tan71°≈2.90)
,sin71°≈0.95,tan71°≈2.90)

查看答案和解析>>
科目:初中数学 来源: 题型:
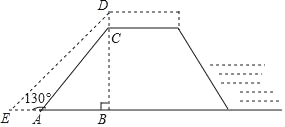
【题目】为做好防汛工作,防汛指挥部决定对某水库的水坝进行加高加固,专家提供的方案是:水坝加高2米(即CD=2米),背水坡DE的坡度i=1:1(即DB:EB=1:1),如图所示,已知AE=4米,∠EAC=130°,求水坝原来的高度BC.(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.2)
查看答案和解析>>
科目:初中数学 来源: 题型:
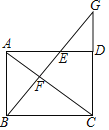
【题目】如图,在矩形ABCD中,AC为对角线,过点B作BF⊥AC于点F,延长BF交AD于点E,交CD的延长线于点G.
(1)求证:△ABF∽△EGD;
(2)若CD=5,DG=3,求tan∠GBC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某经销商销售一种产品,这种产品的成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示:
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)求每天的销售利润W(元)与销售价x(元/千克)之间的函数关系式.当销售价为多少时,每天的销售利润最大?最大利润是多少?
(3)该经销商想要每天获得150元的销售利润,销售价应定为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义[a,b,c]为函数y=ax2+bx+c的特征数,下面给出特征数为[2m,1﹣m,﹣1﹣m]的函数的一些结论,其中不正确的是( )
A. 当m=﹣3时,函数图象的顶点坐标是(![]() ,
,![]() )
)
B. 当m>0时,函数图象截x轴所得的线段长度大于![]()
C. 当m≠0时,函数图象经过同一个点
D. 当m<0时,函数在x>![]() 时,y随x的增大而减小
时,y随x的增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论:①b2>4ac;②2a+b=0;③a+b+c>0;④若点B(-![]() ,y1),C(-
,y1),C(-![]() ,y2)为函数图象上的两点,则y1<y2.其中正确结论是___________.
,y2)为函数图象上的两点,则y1<y2.其中正确结论是___________.
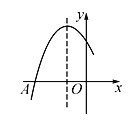
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com