
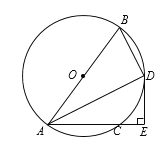
【题目】如图,△ABC内接于⊙O,直径AD交BC于点E,延长AD至点F,使DF=2OD,连接FC并延长交过点A的切线于点G,且满足AG∥BC,连接OC,若cos∠BAC=![]() ,BC=6.
,BC=6.
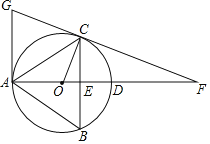
(1)求证:∠COD=∠BAC;
(2)求⊙O的半径OC;
(3)求证:CF是⊙O的切线.
【答案】(1)见解析;(2)![]() ;(3)见解析
;(3)见解析
【解析】
(1)由AG是⊙O的切线得到∠GAF=90°,再由AG∥BC得出AE⊥BC,符合垂径定理,得出∠BAC=2∠EAC,由圆周角定理得到∠COE=2∠CAE,于是可证;
(2)由题意可得![]() =
=![]() ,设OE=x,则OC=3x,根据勾股定理列方程x2+32=9x2,解出即可;
,设OE=x,则OC=3x,根据勾股定理列方程x2+32=9x2,解出即可;
(3)由题意可证明![]() ,再证△COE∽△FOC,于是可得∠OCF=∠DEC=90°,故可证CF是⊙O的切线.
,再证△COE∽△FOC,于是可得∠OCF=∠DEC=90°,故可证CF是⊙O的切线.
解:(1)∵AG是⊙O的切线,AD是⊙O的直径,
∴∠GAF=90°,
∵AG∥BC,
∴AE⊥BC,
∴![]() ,
,
∴∠BAC=2∠EAC,
∵∠COE=2∠CAE,
∴∠COD=∠BAC;
(2)∵∠COD=∠BAC,
∴cos∠BAC=cos∠COE=![]() =
=![]() ,
,
∴设OE=x,OC=3x,
∵BC=6,
∴CE=3,
∵CE⊥AD,
∴OE2+CE2=OC2,
∴x2+32=9x2,
∴x=![]() (负值舍去),
(负值舍去),
∴OC=3x=![]() ,
,
∴⊙O的半径OC为![]() ;
;
(3)∵DF=2OD,
∴OF=3OD=3OC,
∴![]() ,
,
∵∠COE=∠FOC,
∴△COE∽△FOC,
∴∠OCF=∠DEC=90°,
∴CF是⊙O的切线.


科目:初中数学 来源: 题型:
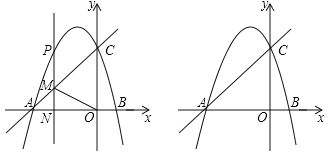
【题目】如图,抛物线y=﹣![]() x2+bx+c与x轴交于A、B两点,与y轴交于C.直线y=
x2+bx+c与x轴交于A、B两点,与y轴交于C.直线y=![]() x+3经过点A、C.
x+3经过点A、C.
(1)求抛物线的解析式;
(2)P是抛物线上一动点,过P作PM∥y轴交直线AC于点M,设点P的横坐标为t.
①若以点C、O、M、P为顶点的四边形是平行四边形,求t的值.
②当射线MP,AC,MO中一条射线平分另外两条射线的夹角时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋中有标号为1,2,3,4的四个小球,除数字不同外,小球没有任何区别,摸球前先搅拌均匀,每次摸一个球
(1)摸出一个球,摸到标号为偶数的概率为 .
(2)从袋中不放回地摸两次,用列表或树状图求出两球标号数字为一奇一偶的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,l1、l2、l3两两相交于A、B、C三点,它们与y轴正半轴分别交于点D、E、F,若A、B、C三点的坐标分别为(1,yA)、(2,yB)、(3,yC),且OD=DE=1,则下列结论正确的个数是( )①EC=3EA,②S△ABC=1,③OF=5,④2yA﹣yA﹣yC=2
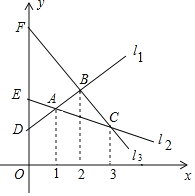
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB=26,P是AB上(不与点A,B重合)的任一点,点C,D为⊙O上的两点.若∠APD=∠BPC,则称∠DPC为直径AB的“回旋角”.
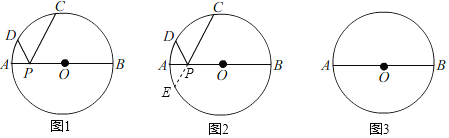
(1)若∠BPC=∠DPC=60°,则∠DPC是直径AB的“回旋角”吗?并说明理由;
(2)猜想回旋角”∠DPC的度数与弧CD的度数的关系,给出证明(提示:延长CP交⊙O于点E);
(3)若直径AB的“回旋角”为120°,且△PCD的周长为24+13![]() ,直接写出AP的长.
,直接写出AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育用品商场预测某品牌运动服能够畅销,就用32000元购进了一批这种运动服,上市后很快脱销,商场又用68000元购进第二批这种运动服,所购数量是第一批购进数量的2倍,但每套进价多了10元.
(1)该商场两次共购进这种运动服多少套?
(2)如果这两批运动服每套的售价相同,且全部售完后总利润不低于20%,那么每套售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC是⊙O的弦,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E,连接BD.
(1)求证:DE是⊙O的切线;
(2)若BD=3,AD=4,则DE= .
查看答案和解析>>
科目:初中数学 来源: 题型:
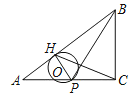
【题目】如图,在△ABC中,∠ACB=90°,AC=4,BC=3,P是AC上的一点,PH⊥AB于点H,以PH为直径作⊙O,当CH与PB的交点落在⊙O上时,AP的值为( )
A.![]() B.
B.![]() C.2D.3
C.2D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年,国家卫生健康委员会和国家教育部在全国开展了儿童青少年近视调查工作,调查数据显示,全国儿童青少年近视过半.某校初三学习小组为了解本校学生对自己视力保护的重视程度,随机在校内调查了部分学生,调查结果分为“非常重视”“重视”“比较重视”“不重视”四类,并将结果绘制成下面的两幅不完整的统计图:
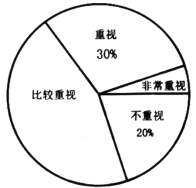
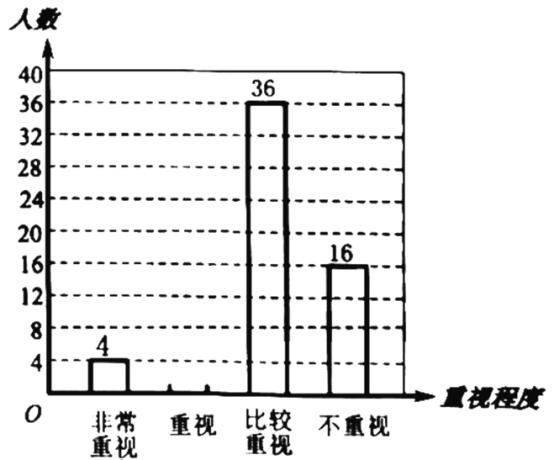
根据图中信息,解答下列问题:
(1)求本次调查的学生总人数,并补全条形统计图;
(2)该校共有学生1000人,请你估计该校对视力保护“非常重视”的学生人数;
(3)对视力“非常重视”的4人有![]() ,
,![]() 两名男生,
两名男生,![]() ,
,![]() 两名女生,若从中随机抽取两人向全校作视力保护交流,请利用树状图或列表的方法,求恰好抽到一男一女的概率.
两名女生,若从中随机抽取两人向全校作视力保护交流,请利用树状图或列表的方法,求恰好抽到一男一女的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com