
ЁОЬтФПЁПШчЭМЃЌЁбOЕФжБОЖABЃН26ЃЌPЪЧABЩЯЃЈВЛгыЕуAЃЌBжиКЯЃЉЕФШЮвЛЕуЃЌЕуCЃЌDЮЊЁбOЩЯЕФСНЕуЃЎШєЁЯAPDЃНЁЯBPCЃЌдђГЦЁЯDPCЮЊжБОЖABЕФЁАЛиа§НЧЁБЃЎ
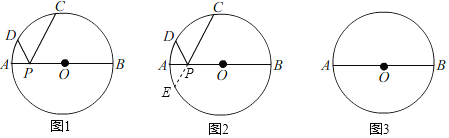
ЃЈ1ЃЉШєЁЯBPCЃНЁЯDPCЃН60ЁуЃЌдђЁЯDPCЪЧжБОЖABЕФЁАЛиа§НЧЁБТ№ЃПВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉВТЯыЛиа§НЧЁБЁЯDPCЕФЖШЪ§гыЛЁCDЕФЖШЪ§ЕФЙиЯЕЃЌИјГіжЄУїЃЈЬсЪОЃКбгГЄCPНЛЁбOгкЕуEЃЉЃЛ
ЃЈ3ЃЉШєжБОЖABЕФЁАЛиа§НЧЁБЮЊ120ЁуЃЌЧвЁїPCDЕФжмГЄЮЊ24+13![]() ЃЌжБНгаДГіAPЕФГЄЃЎ
ЃЌжБНгаДГіAPЕФГЄЃЎ
ЁОД№АИЁПЃЈ1ЃЉЁЯDPCЪЧжБОЖABЕФЛиа§НЧЃЌРэгЩМћНтЮіЃЛЃЈ2ЃЉЁАЛиа§НЧЁБЁЯCPDЕФЖШЪ§ЃН![]() ЕФЖШЪ§ЃЌжЄУїМћНтЮіЃЛЃЈ3ЃЉ3Лђ23ЃЎ
ЕФЖШЪ§ЃЌжЄУїМћНтЮіЃЛЃЈ3ЃЉ3Лђ23ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЁЯBPCЃНЁЯDPCЃН60ЁуНсКЯЦННЧЃН180ЁуЃЌМДПЩЧѓГіЁЯAPDЃН60ЁуЃНЁЯBPCЃЌНјЖјПЩЫЕУїЁЯDPCЪЧжБОЖABЕФЛиа§НЧЃЛ
ЃЈ2ЃЉбгГЄCPНЛдВOгкЕуEЃЌСЌНгODЃЌOCЃЌOEЃЌгЩЁАЛиа§НЧЁБЕФЖЈвхНсКЯЖдЖЅНЧЯрЕШЃЌПЩЕУГіЁЯAPEЃНЁЯAPDЃЌгЩдВЕФЖдГЦадПЩЕУГіЁЯEЃНЁЯDЃЌгЩЕШбќШ§НЧаЮЕФаджЪПЩЕУГіЁЯEЃНЁЯCЃЌНјЖјПЩЕУГіЁЯDЃНЁЯCЃЌРћгУШ§НЧаЮФкНЧКЭЖЈРэПЩЕУГіЁЯCODЃНЁЯCPDЃЌМДЁАЛиа§НЧЁБЁЯCPDЕФЖШЪ§ЃН![]() ЕФЖШЪ§ЃЛ
ЕФЖШЪ§ЃЛ
ЃЈ3ЃЉЂйЕБЕуPдкАыОЖOAЩЯЪБЃЌдкЭМ3жаЃЌЙ§ЕуFзїCFЁЭABЃЌНЛдВOгкЕуFЃЌСЌНгPFЃЌдђPFЃНPCЃЌРћгУЃЈ2ЃЉЕФЗНЗЈПЩЕУГіЕуPЃЌDЃЌFдкЭЌвЛЬѕжБЯпЩЯЃЌгЩжБОЖABЕФЁАЛиа§НЧЁБЮЊ120ЁуЃЌПЩЕУГіЁЯAPDЃНЁЯBPCЃН30ЁуЃЌНјЖјПЩЕУГіЁЯCPFЃН60ЁуЃЌМДЁїPFCЪЧЕШБпШ§НЧаЮЃЌИљОнЕШБпШ§НЧаЮЕФаджЪПЩЕУГіЁЯCFDЃН60ЁуЃЎСЌНгOCЃЌODЃЌЙ§ЕуOзїOGЁЭCDгкЕуGЃЌдђЁЯCODЃН120ЁуЃЌИљОнЕШбќШ§НЧаЮЕФаджЪПЩЕУГіCDЃН2DGЃЌЁЯDOGЃН![]() ЁЯCODЃН60ЁуЃЌНсКЯдВЕФжБОЖЮЊ26ПЩЕУГіCDЃН13
ЁЯCODЃН60ЁуЃЌНсКЯдВЕФжБОЖЮЊ26ПЩЕУГіCDЃН13![]() ЃЌгЩЁїPCDЕФжмГЄЮЊ24+13
ЃЌгЩЁїPCDЕФжмГЄЮЊ24+13![]() ЃЌПЩЕУГіDFЃН24ЃЌЙ§ЕуOзїOHЁЭDFгкЕуHЃЌдкRtЁїOHDКЭдкRtЁїOHDжаЃЌЭЈЙ§НтжБНЧШ§НЧаЮПЩЕУГіOHЃЌOPЕФжЕЃЌдйИљОнAPЃНOAЉOPПЩЧѓГіAPЕФжЕЃЛЂкЕБЕуPдкАыОЖOBЩЯЪБЃЌгУЂйЕФЗНЗЈЃЌПЩЕУЃКBPЃН3ЃЌдйИљОнAPЃНABЉBPПЩЧѓГіAPЕФжЕЃЎзлЩЯМДПЩЕУГіНсТлЃЎ
ЃЌПЩЕУГіDFЃН24ЃЌЙ§ЕуOзїOHЁЭDFгкЕуHЃЌдкRtЁїOHDКЭдкRtЁїOHDжаЃЌЭЈЙ§НтжБНЧШ§НЧаЮПЩЕУГіOHЃЌOPЕФжЕЃЌдйИљОнAPЃНOAЉOPПЩЧѓГіAPЕФжЕЃЛЂкЕБЕуPдкАыОЖOBЩЯЪБЃЌгУЂйЕФЗНЗЈЃЌПЩЕУЃКBPЃН3ЃЌдйИљОнAPЃНABЉBPПЩЧѓГіAPЕФжЕЃЎзлЩЯМДПЩЕУГіНсТлЃЎ
ЃЈ1ЃЉЁпЁЯBPCЃНЁЯDPCЃН60ЁуЃЌ
ЁрЁЯAPDЃН180ЁуЉЁЯBPCЉЁЯDPCЃН180ЁуЉ60ЁуЉ60ЁуЃН60ЁуЃЌ
ЁрЁЯAPDЃНЁЯBPCЃЌ
ЁрЁЯDPCЪЧжБОЖABЕФЛиа§НЧЃЎ
ЃЈ2ЃЉЁАЛиа§НЧЁБЁЯCPDЕФЖШЪ§ЃН![]() ЕФЖШЪ§ЃЌРэгЩШчЯТЃК
ЕФЖШЪ§ЃЌРэгЩШчЯТЃК
ШчЭМ2ЃЌбгГЄCPНЛдВOгкЕуEЃЌСЌНгODЃЌOCЃЌOEЃЎ

ЁпЁЯCPBЃНЁЯAPEЃЌЁЯAPDЃНЁЯCPBЃЌ
ЁрЁЯAPEЃНЁЯAPDЃЎ
ЁпдВЪЧжсЖдГЦЭМаЮЃЌ
ЁрЁЯEЃНЁЯDЃЎ
ЁпOEЃНOCЃЌ
ЁрЁЯEЃНЁЯCЃЌ
ЁрЁЯDЃНЁЯCЃЎ
гЩШ§НЧаЮФкНЧКЭЖЈРэЃЌПЩжЊЃКЁЯCODЃНЁЯCPDЃЌ
ЁрЁАЛиа§НЧЁБЁЯCPDЕФЖШЪ§ЃН![]() ЕФЖШЪ§ЃЎ
ЕФЖШЪ§ЃЎ
ЃЈ3ЃЉЂйЕБЕуPдкАыОЖOAЩЯЪБЃЌдкЭМ3жаЃЌЙ§ЕуFзїCFЁЭABЃЌНЛдВOгкЕуFЃЌСЌНгPFЃЌдђPFЃНPCЃЎ
ЭЌЃЈ2ЃЉЕФЗНЗЈПЩЕУЃКЕуPЃЌDЃЌFдкЭЌвЛЬѕжБЯпЩЯЃЎ
ЁпжБОЖABЕФЁАЛиа§НЧЁБЮЊ120ЁуЃЌ
ЁрЁЯAPDЃНЁЯBPCЃН30ЁуЃЌ
ЁрЁЯCPFЃН60ЁуЃЌ
ЁрЁїPFCЪЧЕШБпШ§НЧаЮЃЌ
ЁрЁЯCFDЃН60ЁуЃЎ
СЌНгOCЃЌODЃЌЙ§ЕуOзїOGЁЭCDгкЕуGЃЌдђЁЯCODЃН120ЁуЃЌ
ЁрCDЃН2DGЃЌЁЯDOGЃН![]() ЁЯCODЃН60ЁуЃЌ
ЁЯCODЃН60ЁуЃЌ
ЁпAB=26ЃЌ
ЁрOC=13ЃЌ
Ёр![]()
ЁрCDЃН2ЁС![]() ЃН
ЃН![]() .
.
ЁпЁїPCDЕФжмГЄЮЊ24+![]() ЃЌ
ЃЌ
ЁрPD+PC+CDЃН24+![]() ЃЌ
ЃЌ
ЁрPD+PCЃНDFЃН24ЃЎ
Й§ЕуOзїOHЁЭDFгкЕуHЃЌдђDHЃНFHЃН![]() DFЃН12ЃЎ
DFЃН12ЃЎ
дкRtЁїOHDжаЃЌOHЃН![]() ,
,
дкRtЁїOHPжаЃЌЁЯOPHЃН30ЁуЃЌ
ЁрOPЃН2OHЃН10ЃЌ
ЁрAPЃНOAЉOPЃН13Љ10ЃН3ЃЛ
ЂкЕБЕуPдкАыОЖOBЩЯЪБЃЌ
ЭЌЂйЕФЗНЗЈЃЌПЩЕУЃКBPЃН3ЃЌ
ЁрAPЃНABЉBPЃН26Љ3ЃН23ЃЎ
злЩЯЫљЪіЃЌAPЕФГЄЮЊЃК3Лђ23ЃЎ


 ЬвРюЮФЛЏПьРжЪюМйЮфККГіАцЩчЯЕСаД№АИ
ЬвРюЮФЛЏПьРжЪюМйЮфККГіАцЩчЯЕСаД№АИ гХауЩњПьРжМйЦкУПвЛЬьШЋаТКЎМйзївЕБОЯЕСаД№АИ
гХауЩњПьРжМйЦкУПвЛЬьШЋаТКЎМйзївЕБОЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
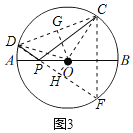
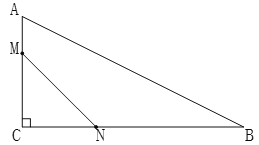
ЁОЬтФПЁПвбжЊABЪЧАыдВOЕФжБОЖЃЌMЃЌNЪЧАыдВЩЯВЛгыAЃЌBжиКЯЕФСНЕуЃЌЧвЕуNдк![]() ЩЯ.
ЩЯ.
ЃЈ1ЃЉШчЭМ1ЃЌMAЃН6ЃЌMBЃН8ЃЌЁЯNOBЃН60ЁуЃЌЧѓNBЕФГЄЃЛ

ЃЈ2ЃЉШчЭМ2ЃЌЙ§ЕуMзїMCЁЭABгкЕуCЃЌPЪЧMNЕФжаЕуЃЌСЌНгMBЃЌNAЃЌPCЃЌЪдЬНОПЁЯMCPЃЌЁЯNABЃЌЁЯMBAжЎМфЕФЪ§СПЙиЯЕЃЌВЂжЄУї.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
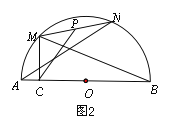
ЁОЬтФПЁПШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌЕуCЪЧЁбOЩЯвЛЕуЃЌ![]() ЃЌЕуDЪЧABЩЯвЛЕуЃЈЕуDгыAЃЌBВЛжиКЯЃЉЃЌСЌНгCDЃЎ
ЃЌЕуDЪЧABЩЯвЛЕуЃЈЕуDгыAЃЌBВЛжиКЯЃЉЃЌСЌНгCDЃЎ
ЃЈ1ЃЉгУГпЙцзїЭМЃЌЯпЖЮCDШЦЕуCАДФцЪБеыЗНЯђа§зЊ90ЁуЕУЕНЯпЖЮCEЃЌСЌНгDEНЛBCгкЕуFЃЌСЌНгBEЃЛЃЈБЃСєзїЭМКлМЃЃЌВЛаДзїЗЈЃЎЃЉ
ЃЈ2ЃЉЕБADЃНBFЪБЃЌЧѓЁЯBEFЕФЖШЪ§ЃЎ
ЃЈ3ЃЉЧѓжЄЃКAD2+BD2ЃН2CD2ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЙћХЉдкЦфГаАќЕФЙћдАжажжжВСЫ60ПУНлзгЪїЃЌУППУНлзгЪїЕФВњСПЪЧ100kgЃЌЙћХЉЯыдіМгНлзгЪїЕФПУЪ§РДдіВњЃЌЕЋдіМгЙћЪїЛсЕМжТУППУЪїЕФЙтееМѕЩйЃЌЪЙЕУЕЅПУЙћЪїВњСПМѕЩйЃЌЪдбщЗЂЯжУПдіМг1ПУНлзгЪїЃЌЕЅПУНлзгЪїЕФВњСПМѕЩй0.5kg.
(1)дкЭЖШыГЩБОзюЕЭЕФЧщПіЯТЃЌдіМгЖрЩйПУНлзгЪїЪБЃЌПЩвдЪЙЙћдАзмВњСПДяЕН6650kgЃП
(2)ЩшдіМгxПУНлзгЪїЃЌПМТЧЪЕМЪдіМгНлзгЪїЕФЧщПіЃЌ10ЁмxЁм40ЃЌЧыФуМЦЫувЛЯТЃЌЙћдАзмВњСПзюЖрЮЊЖрЩйkgЃЌзюЩйЮЊЖрЩйkgЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
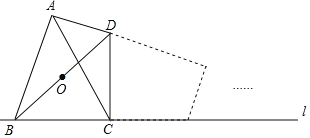
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDжаЃЌЁЯBADЃНЁЯBCDЃН90ЁуЃЌACЦНЗжЁЯBADЃЌACЃН7ЃЌADЃН3![]() ЃЌНЋЫФБпаЮABCDбижБЯпlЮоЛЌЖЏЗЙівЛжмЃЌдђЖдНЧЯпBDЕФжаЕуOОЙ§ЕФТЗОЖГЄЖШЮЊ_____ЃЎ
ЃЌНЋЫФБпаЮABCDбижБЯпlЮоЛЌЖЏЗЙівЛжмЃЌдђЖдНЧЯпBDЕФжаЕуOОЙ§ЕФТЗОЖГЄЖШЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
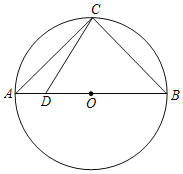
ЁОЬтФПЁПШчЭМЃЌЁїABCФкНггкЁбOЃЌжБОЖADНЛBCгкЕуEЃЌбгГЄADжСЕуFЃЌЪЙDFЃН2ODЃЌСЌНгFCВЂбгГЄНЛЙ§ЕуAЕФЧаЯпгкЕуGЃЌЧвТњзуAGЁЮBCЃЌСЌНгOCЃЌШєcosЁЯBACЃН![]() ЃЌBCЃН6ЃЎ
ЃЌBCЃН6ЃЎ
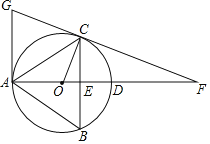
ЃЈ1ЃЉЧѓжЄЃКЁЯCODЃНЁЯBACЃЛ
ЃЈ2ЃЉЧѓЁбOЕФАыОЖOCЃЛ
ЃЈ3ЃЉЧѓжЄЃКCFЪЧЁбOЕФЧаЯпЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпyЃНax2+bx+cЃЈaЁй0ЃЉгыyжсНЛгкЕуCЃЈ0ЃЌ4ЃЉЃЌгыxжсНЛгкAЃЈЉ2ЃЌ0ЃЉЃЌЕуBЃЈ4ЃЌ0ЃЉЃЎ

ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєЕуMЪЧХзЮяЯпЩЯЕФвЛЖЏЕуЃЌЧвдкжБЯпBCЕФЩЯЗНЃЌЕБSЁїMBCШЁЕУзюДѓжЕЪБЃЌЧѓЕуMЕФзјБъЃЛ
ЃЈ3ЃЉдкжБЯпЕФЩЯЗНЃЌХзЮяЯпЪЧЗёДцдкЕуMЃЌЪЙЫФБпаЮABMCЕФУцЛ§ЮЊ15ЃПШєДцдкЃЌЧѓГіЕуMЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЖЏЕу
ЃЌЖЏЕу![]() Дг
Дг![]() ЕуГіЗЂЃЌвдУПУы
ЕуГіЗЂЃЌвдУПУы![]() ИіЕЅЮЛГЄЖШЕФЫйЖШбизХ
ИіЕЅЮЛГЄЖШЕФЫйЖШбизХ![]() ЗНЯђЯђ
ЗНЯђЯђ![]() ЕудЫЖЏЃЌЖЏЕу
ЕудЫЖЏЃЌЖЏЕу![]() Дг
Дг![]() ЕуГіЗЂЃЌвдУПУы
ЕуГіЗЂЃЌвдУПУы![]() ИіЕЅЮЛГЄЖШЕФЫйЖШбизХ
ИіЕЅЮЛГЄЖШЕФЫйЖШбизХ![]() ЗНЯђЯђ
ЗНЯђЯђ![]() ЕудЫЖЏЃЌШчЙћ
ЕудЫЖЏЃЌШчЙћ![]() ЃЌ
ЃЌ![]() СНЕуЭЌЪБГіЗЂЃЌЕБ
СНЕуЭЌЪБГіЗЂЃЌЕБ![]() ЕНДя
ЕНДя![]() ЕуДІЪБЃЌСНЕуЖМЭЃжЙдЫЖЏ.ЩшдЫЖЏЕФЪБМфЮЊ
ЕуДІЪБЃЌСНЕуЖМЭЃжЙдЫЖЏ.ЩшдЫЖЏЕФЪБМфЮЊ![]() УыЃЌ
УыЃЌ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() .
.
ЃЈ1ЃЉгУКЌ![]() ЕФДњЪ§ЪНБэЪОЃК
ЕФДњЪ§ЪНБэЪОЃК
![]() ,
,![]() ЃЌ
ЃЌ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЧѓ![]() ЕФзюДѓжЕ.
ЕФзюДѓжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкДШЩЦвЛШеОшЛюЖЏжаЃЌбЇаЃЭХзмжЇЮЊСЫСЫНтБОаЃбЇЩњЕФОшПюЧщПіЃЌЫцЛњГщШЁСЫ50УћбЇЩњЕФОшПюЪ§НјааСЫЭГМЦЃЌВЂЛцжЦГЩЯТУцЕФЭГМЦЭМЃЎ
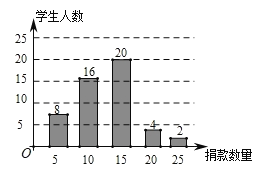
ЃЈ1ЃЉет50УћЭЌбЇОшПюЕФжкЪ§ЮЊЁЁЁЁЁЁЁЁ дЊЃЌжаЮЛЪ§ЮЊЁЁЁЁЁЁЁЁ дЊЃЛ
ЃЈ2ЃЉИУаЃЙВга600УћбЇЩњВЮгыОшПюЃЌЧыЙРМЦИУаЃбЇЩњЕФОшПюзмЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com