
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,![]() ,点D是AB上一点(点D与A,B不重合),连接CD.
,点D是AB上一点(点D与A,B不重合),连接CD.
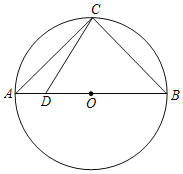
(1)用尺规作图,线段CD绕点C按逆时针方向旋转90°得到线段CE,连接DE交BC于点F,连接BE;(保留作图痕迹,不写作法.)
(2)当AD=BF时,求∠BEF的度数.
(3)求证:AD2+BD2=2CD2.
【答案】(1)如图,见解析;CE、BE为所作;(2)∠BEF=67.5°;(3)见解析.
【解析】
(1)延长线段DC,以C为圆心,以适当的长为半径画弧交CD于两点M、N.2)分别以两点为圆心,以大于二分之一MN同样长为半径画弧,两弧交于P,作射线CP,以C为圆心,以CD长为半径作弧,交射线CP与点E,连接BE即可.
(2)根据圆中,直径对直角推导出,△ACB为等腰直角三角形,根据旋转的性质得到,CD=CE,∠ACD=∠BCE,由此判断呢△ACD≌△BCE,得到∠CBE=∠A=45°,再根据AD=BF推出∠BEF=∠BFE,最后计算∠BEF的度数即可.
(3)根据勾股定理可得BE2+DB2=DE2,根据题意和直角三角形的边角关系可得BE=AD,DE=![]() CD,然后换算解决即可.
CD,然后换算解决即可.
(1)解:如图,CE、BE为所作;
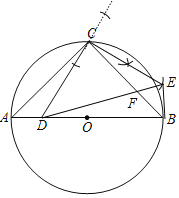
(2)解:∵AB为直径,
∴∠ACB=90°,
∵![]() ,
,
∴AC=BC,
∴△ACB为等腰直角三角形,
∴∠A=∠ABC=45°,
∵线段CD绕点C按逆时针方向旋转90°得到线段CE,
∴∠DCE=90°,CD=CE,
∴∠ACD=∠BCE,
在△ACD和△BCE中
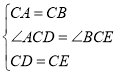 ,
,
∴△ACD≌△BCE(SAS),
∴AD=BE,∠CBE=∠A=45°,
∵AD=BF,
∴BF=BE,
∴∠BEF=∠BFE,
∴∠BEF=![]() (180°﹣45°)=67.5°;
(180°﹣45°)=67.5°;
(3)证明:∵∠ABC=45°,∠CBE=45°,
∴∠DBE=90°,
∴BE2+DB2=DE2,
∵BE=AD,DE=![]() CD,
CD,
∴AD2+BD2=2CD2.


科目:初中数学 来源: 题型:
【题目】海中有一个小岛P,它的周围18海里内有暗礁,渔船跟踪鱼群由西向东航行,在点A测得小岛P在北偏东60°方向上,航行12海里到达B点,这时测得小岛P在北偏东45°方向上.如果渔船不改变航线继续向东航行,有没有触礁危险?请说明理由.
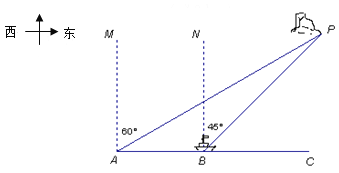
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
(1)求证:△ADE∽△ABC;
(2)若AD=3,AB=5,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点 C 为 Rt△ACB 与 Rt△DCE 的公共点,∠ACB=∠DCE=90°,连 接 AD、BE,过点 C 作 CF⊥AD 于点 F,延长 FC 交 BE 于点 G.若 AC=BC=25,CE=15, DC=20,则![]() 的值为___________.
的值为___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠B=60°,BC=2.将△ABC绕点C顺时针旋转,得到△A′B′C,连接AB′,且A,B′,A′在同一条直线上,则AA′=_____.
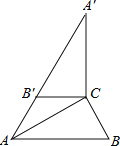
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋中有标号为1,2,3,4的四个小球,除数字不同外,小球没有任何区别,摸球前先搅拌均匀,每次摸一个球
(1)摸出一个球,摸到标号为偶数的概率为 .
(2)从袋中不放回地摸两次,用列表或树状图求出两球标号数字为一奇一偶的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 过点(1,0)和点(0,-3),且顶点在第三象限,设m=a-b+c,则m的取值范围是( )
过点(1,0)和点(0,-3),且顶点在第三象限,设m=a-b+c,则m的取值范围是( )
A.-6<m<0B.-6<m<-3C.-3<m<0D.-3<m<-1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB=26,P是AB上(不与点A,B重合)的任一点,点C,D为⊙O上的两点.若∠APD=∠BPC,则称∠DPC为直径AB的“回旋角”.
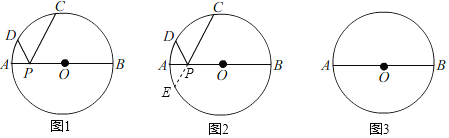
(1)若∠BPC=∠DPC=60°,则∠DPC是直径AB的“回旋角”吗?并说明理由;
(2)猜想回旋角”∠DPC的度数与弧CD的度数的关系,给出证明(提示:延长CP交⊙O于点E);
(3)若直径AB的“回旋角”为120°,且△PCD的周长为24+13![]() ,直接写出AP的长.
,直接写出AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点C、D都在⊙O上,且CD平分∠ACB,交AB于点E.
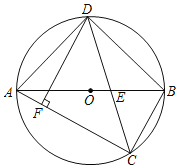
(1)求证:∠ABD=∠BCD;
(2)若DE=13,AE=17,求⊙O的半径;
(3)DF⊥AC于点F,试探究线段AF、DF、BC之间的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com