
【题目】已知AB是半圆O的直径,M,N是半圆上不与A,B重合的两点,且点N在![]() 上.
上.
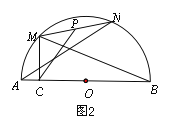
(1)如图1,MA=6,MB=8,∠NOB=60°,求NB的长;

(2)如图2,过点M作MC⊥AB于点C,P是MN的中点,连接MB,NA,PC,试探究∠MCP,∠NAB,∠MBA之间的数量关系,并证明.
【答案】(1)5;(2)∠MCP+∠MBA+∠NAB=90°,证明见解析
【解析】
(1)只要证明△OBN是等边三角形即可解决问题;
(2)结论:∠MCP+∠MBA+∠NAB=90°.如图2中,画⊙O,延长MC交⊙O于点Q,连接NQ,NB.关键是证明CP∥QN.
(1)如图1,∵AB是半圆O的直径,
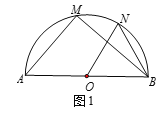
∴∠M=90°.
在Rt△AMB中,AB=![]()
∴AB=10.
∴OB=5.
∵OB=ON,
又∵∠NOB=60°,
∴△NOB是等边三角形.
∴NB=OB=5.
(2)证明:如图2,
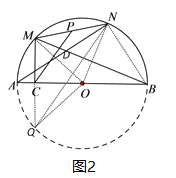
画⊙O,延长MC交⊙O于点Q,连接NQ,NB.
∵MC⊥AB,
又∵OM=OQ,
∴MC=CQ.
即C是MN的中点
又∵P是MQ的中点,
∴CP是△MQN的中位线.
∴CP∥QN.
∴∠MCP=∠MQN.
∵∠MQN=![]() ∠MON,∠MBN=
∠MON,∠MBN=![]() ∠MON,
∠MON,
∴∠MQN=∠MBN.
∴∠MCP=∠MBN.
∵AB是直径,
∴∠ANB=90°.
∴在△ANB中,∠NBA+∠NAB=90°.
∴∠MBN+∠MBA+∠NAB=90°.
即∠MCP+∠MBA+∠NAB=90°


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点E在⊙O上,C为![]() 的中点,过点C作直线CD⊥AE于D,连接AC,BC.
的中点,过点C作直线CD⊥AE于D,连接AC,BC.
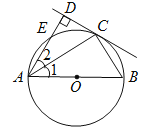
(1)试判断直线CD与⊙O的位置关系,并说明理由;
(2)若AD=2,AC=![]() ,求AB的长.
,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
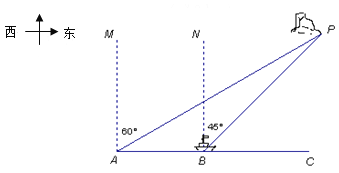
【题目】海中有一个小岛P,它的周围18海里内有暗礁,渔船跟踪鱼群由西向东航行,在点A测得小岛P在北偏东60°方向上,航行12海里到达B点,这时测得小岛P在北偏东45°方向上.如果渔船不改变航线继续向东航行,有没有触礁危险?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
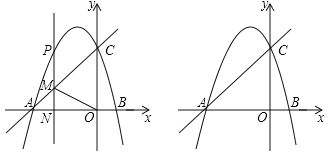
【题目】如图,抛物线y=﹣![]() x2+bx+c与x轴交于A、B两点,与y轴交于C.直线y=
x2+bx+c与x轴交于A、B两点,与y轴交于C.直线y=![]() x+3经过点A、C.
x+3经过点A、C.
(1)求抛物线的解析式;
(2)P是抛物线上一动点,过P作PM∥y轴交直线AC于点M,设点P的横坐标为t.
①若以点C、O、M、P为顶点的四边形是平行四边形,求t的值.
②当射线MP,AC,MO中一条射线平分另外两条射线的夹角时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
(1)求证:△ADE∽△ABC;
(2)若AD=3,AB=5,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点 C 为 Rt△ACB 与 Rt△DCE 的公共点,∠ACB=∠DCE=90°,连 接 AD、BE,过点 C 作 CF⊥AD 于点 F,延长 FC 交 BE 于点 G.若 AC=BC=25,CE=15, DC=20,则![]() 的值为___________.
的值为___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB=26,P是AB上(不与点A,B重合)的任一点,点C,D为⊙O上的两点.若∠APD=∠BPC,则称∠DPC为直径AB的“回旋角”.
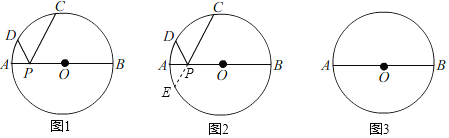
(1)若∠BPC=∠DPC=60°,则∠DPC是直径AB的“回旋角”吗?并说明理由;
(2)猜想回旋角”∠DPC的度数与弧CD的度数的关系,给出证明(提示:延长CP交⊙O于点E);
(3)若直径AB的“回旋角”为120°,且△PCD的周长为24+13![]() ,直接写出AP的长.
,直接写出AP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com