
【题目】已知点A(2,a)在抛物线y=x2上
(1)求A点的坐标;
(2)在x轴上是否存在点P,使△OAP是等腰三角形?若存在写出P点坐标;若不存在,说明理由.
【答案】
(1)
解:∵点A(2,a)在抛物线y=x2上,
∴a=22=4,
∴A点的坐标为:(2,4);
(2)
解:如图所示:
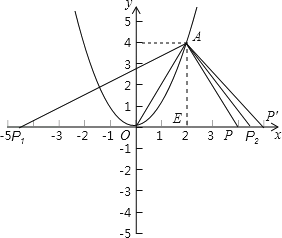
以O为顶点时,
AO=P1O= ![]() 或AO=AP2=
或AO=AP2= ![]()
∴点P坐标:( ![]() ,0),(﹣
,0),(﹣ ![]() ,0),
,0),
以A为顶点时,AO=OP,
∴点P坐标:(4,0);
以P为顶点时,OP′=AP′,
∴AE2+P′E2=P′A2,设AP′=x,
则42+(x﹣2)2=x2,
解得:x=5,
∴点P坐标:(5,0),
综上所述:使△OAP是等腰三角形则P点坐标为:( ![]() ,0),(﹣
,0),(﹣ ![]() ,0),(4,0),(5,0).
,0),(4,0),(5,0).
【解析】(1)直接将A点代入解析式求出即可A点坐标即可;(2)分别根据以O为顶点时,以A为顶点时,以P为顶点时求出符合题意的点的坐标即可.


科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,点P是BA延长线上一点,PC是⊙O的切线,切点为C,过点B作BD⊥PC交PC的延长线于点D,连接BC.求证:
(1)∠PBC=∠CBD;
(2)BC2=ABBD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某风景区门票价格如图所示,百姓旅行社有甲、乙两个旅行团队,计划在“五一”小黄金周期间到该景点游玩,两团队游客人数之和为120人,乙团队人数不超过50人.设甲团队人数为x人,如果甲、乙两团队分别购买门票,两团队门票款之和为W元.
(1)求W关于x的函数关系式,并写出自变量x 的取值范围;
(2)若甲团队人数不超过100人,请说明甲、乙两团队联合购票比分别购票最多可节约多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C,D在⊙O上,且AD平分∠CAB,过点D作AC的垂线,与AC的延长线相交于点E,与AB的延长线相交于点F.
(1)求证:EF与⊙O相切;
(2)若AB=6,AD=4 ![]() ,求EF的长.
,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某数学活动小组要测量楼AB的高度,楼AB在太阳光的照射下在水平面的影长BC为6米,在斜坡CE的影长CD为13米,身高1.5米的小红在水平面上的影长为1.35米,斜坡CE的坡度为1:2.4,求楼AB的高度.(坡度为铅直高度与水平宽度的比)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=﹣x+6,交x轴、y轴于A、B两点,抛物线y=x2+mx+n经过A点,且与直线y=﹣x+6交于另一点P. 
(1)若P与B点重合,求抛物线的解析式;
(2)若P在第一象限,过PE⊥x轴于E点,PF⊥y轴于F点,当四边形PEOF面积为5,求抛物线的解析式;
(3)若△OAP为等腰三角形,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数y=x2﹣3(m﹣1)x+3m﹣4(m为实数)的图象与x轴交于A(x1 , 0)、B(x2 , 0)(x1≠x2)两点.
(1)求m的取值范围;
(2)若 ![]() (O为坐标原点),求m的值.
(O为坐标原点),求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别位于反比例函数y= ![]() ,y=
,y= ![]() 在第一象限图象上的两点A、B,与原点O在同一直线上,且
在第一象限图象上的两点A、B,与原点O在同一直线上,且 ![]() =
= ![]() .
. 
(1)求反比例函数y= ![]() 的表达式;
的表达式;
(2)过点A作x轴的平行线交y= ![]() 的图象于点C,连接BC,求△ABC的面积.
的图象于点C,连接BC,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com