
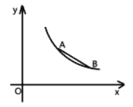
【题目】如图,点A(m,m+1),B(m+3,m-1)都在反比例函数y=![]() 的图象上. 将线段 AB沿直线y=kx+b进行对折得到对应线段A′B′,且点A′ 始终在直线OA上,当线段A′B′ 与x轴有交点时,(1),m=____;(2),b的取值范围是____.
的图象上. 将线段 AB沿直线y=kx+b进行对折得到对应线段A′B′,且点A′ 始终在直线OA上,当线段A′B′ 与x轴有交点时,(1),m=____;(2),b的取值范围是____.
【答案】m=3 ![]() ≤b≤
≤b≤![]() .
.
【解析】
(1)由题可得m(m+1)=(m+3)(m-1),解这个方程就可求出m的值;
(2) 由于点A关于直线y=kx+b的对称点点A1始终在直线OA上,因此直线y=kx+b必与直线OA垂直,只需考虑两个临界位置(A1在x轴上、B1在x轴上)对应的b的值,就可以求出b的取值范围.
(1)∵点A(m,m+1),B(m+3,m-1)都在反比例函数y=![]() 的图象上.
的图象上.
∴m(m+1)=(m+3)(m-1).
解得:m=3.
(2) ①当点B1落到x轴上时,如图1,

设直线OA的解析式为y=ax,
∵点A的坐标为(3,4),
∴3a=4,即a=![]() .
.
∴直线OA的解析式为y=![]() x.
x.
∵点A1始终在直线OA上,
∴直线y=kx+b与直线OA垂直.
∴![]() k=-1.
k=-1.
∴k=-![]() .
.
由于BB1∥OA,因此直线BB1可设为y=![]() x+c.
x+c.
∵点B的坐标为(6,2),
∴![]() ×6+c=2,即c=-6.
×6+c=2,即c=-6.
∴直线BB1解析式为y=![]() x-6.
x-6.
当y=0时,![]() x-6=0.则有x=
x-6=0.则有x=![]() .
.
∴点B1的坐标为(![]() ,0).
,0).
∵点C是BB1的中点,
∴点C的坐标为(![]() ,
,![]() )即(
)即(![]() ,1).
,1).
∵点C在直线y=-![]() x+b上,
x+b上,
∴-![]() ×
×![]() +b=1.
+b=1.
解得:b=![]() .
.
②当点A1落到x轴上时,如图2,

此时,点A1与点O重合.
∵点D是AA1的中点,A(3,4),A1(0,0),
∴D(![]() ,2).
,2).
∵点D在直线y=-![]() x+b上,
x+b上,
∴-![]() ×
×![]() +b=2.
+b=2.
解得:b=![]() .
.
综上所述:当线段A1B1与x轴有交点时,则b的取值范围为![]() ≤b≤
≤b≤![]() .
.
故答案为:![]() ≤b≤
≤b≤![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某市篮球队到市一中选拔一名队员,教练对王亮和李刚两名同学进行![]() 次
次![]() 分投篮测试,一人每次投
分投篮测试,一人每次投![]() 个球,下图记录的是这两名同学
个球,下图记录的是这两名同学![]() 次投篮中所投中的个数.
次投篮中所投中的个数.
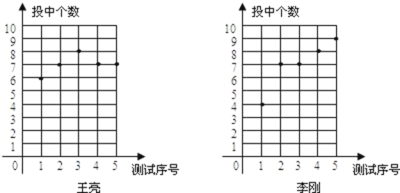
(1)请你根据图中的数据,填写下表;
姓名 | 平均数 | 众数 | 方差 |
王亮 |
| ||
李刚 |
|
|
|
(2)你认为谁的成绩比较稳定,为什么?
(3)若你是教练,你打算选谁?简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
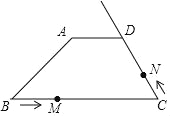
【题目】如图,在四边形ABCD中,AD∥BC,AD=3,DC=5,AB=4![]() ,∠B=45°.动点M从B点出发沿线段BC以每秒2个单位长度的速度向终点C运动;动点N同时从C点出发沿射线CD以每秒1个单位长度的速度运动.设运动的时间为t秒.
,∠B=45°.动点M从B点出发沿线段BC以每秒2个单位长度的速度向终点C运动;动点N同时从C点出发沿射线CD以每秒1个单位长度的速度运动.设运动的时间为t秒.
(1)BC=____.
(2)MC=_____.(用t表示)
(3)求t为何值时,四边形AMCD为平行四边形.
(4)直接写出t为何值时,△AND为直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学数学兴趣小组为了解本校学生对电视节目的喜爱情况,随机调查了部分学生最喜爱哪一类节目(被调查的学生只选一类并且没有不选择的),并将调查结果制成了如下的两个统计图(不完整).请你根据图中所提供的信息,完成下列问题:
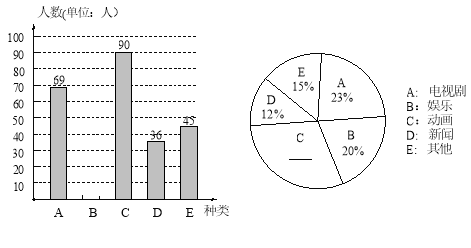
(1)求本次调查的学生人数;
(2)请将两个统计图补充完整,并求出新闻节目在扇形统计图中所占圆心角的度数;
(3)若该中学有2000名学生,请估计该校喜爱电视剧节目的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
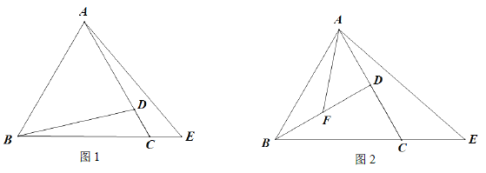
【题目】在等边![]() 中,点D在线段AC上,E为BC延长线上一点,且CD = CE,连接BD,连接AE.
中,点D在线段AC上,E为BC延长线上一点,且CD = CE,连接BD,连接AE.
(1)如图1,若![]() ,求线段AD的长;
,求线段AD的长;
(2)如图2,若F是线段BD的中点,连接AF,若![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在课外学习时遇到这样一个问题:
定义:如果二次函数y=a1x2+b1x+c1(a1≠0,a1,b1,c1是常数)与y=a2x2+b2x+c2(a2≠0,a2,b2,c2是常数)满足a1+a2=0,b1=b2,c1+c2=0,则称这两个函数互为“旋转函数”.
求函数y=﹣x2+3x﹣2的“旋转函数”.
小明是这样思考的:由函数y=﹣x2+3x﹣2可知,a1=﹣1,b1=3,c1=﹣2,根据a1+a2=0,b1=b2,c1+c2=0,求出a2,b2,c2,就能确定这个函数的“旋转函数”.
请参考小明的方法解决下面问题:
(1)写出函数y=﹣x2+3x﹣2的“旋转函数”;
(2)若函数y=﹣x2+![]() mx﹣2与y=x2﹣2nx+n互为“旋转函数”,求(m+n)2015的值;
mx﹣2与y=x2﹣2nx+n互为“旋转函数”,求(m+n)2015的值;
(3)已知函数y=﹣![]() (x+1)(x﹣4)的图象与x轴交于点A、B两点,与y轴交于点C,点A、B、C关于原点的对称点分布是A1,B1,C1,试证明经过点A1,B1,C1的二次函数与函数y=﹣
(x+1)(x﹣4)的图象与x轴交于点A、B两点,与y轴交于点C,点A、B、C关于原点的对称点分布是A1,B1,C1,试证明经过点A1,B1,C1的二次函数与函数y=﹣![]() (x+1)(x﹣4)互为“旋转函数.”
(x+1)(x﹣4)互为“旋转函数.”
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
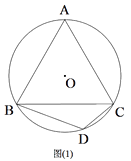
【题目】已知:△ABC是⊙O的内接三角形,且AB=BC,点D为劣弧BC上的一点,连接BD、DC.
(1)如图1,若∠BDC=120°,求证:△ABC是等边三角形;
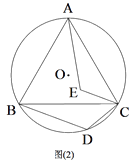
(2)如图2,在(1)的条件下,线段CD绕点C顺时针旋转60°,得到线段CE,连接AE,求证:BD=AE;
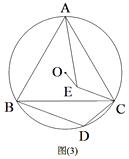
(3)如图3,在(2)的条件下,连接OE,若⊙O的半径为![]() ,OE=2,求BD的长.
,OE=2,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,∠DAB=130°,连结OC,P是半径OC上的一个动点,连结PD、PB,则么DPB的大小可能为( )
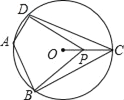
A. 40° B. 80° C. 110° D. 130°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com