
【题目】如图,四边形ABCD内接于⊙O,∠DAB=130°,连结OC,P是半径OC上的一个动点,连结PD、PB,则么DPB的大小可能为( )
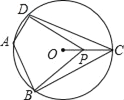
A. 40° B. 80° C. 110° D. 130°
科目:初中数学 来源: 题型:
【题目】如图,点A(m,m+1),B(m+3,m-1)都在反比例函数y=![]() 的图象上. 将线段 AB沿直线y=kx+b进行对折得到对应线段A′B′,且点A′ 始终在直线OA上,当线段A′B′ 与x轴有交点时,(1),m=____;(2),b的取值范围是____.
的图象上. 将线段 AB沿直线y=kx+b进行对折得到对应线段A′B′,且点A′ 始终在直线OA上,当线段A′B′ 与x轴有交点时,(1),m=____;(2),b的取值范围是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,AC平分∠BAD,延长DC交AB的延长线于点E .
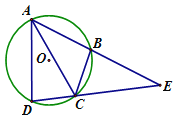
(1)若∠ADC=86°,求∠CBE的度数;
(2)若AC=EC,求证:AD=BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售某种品牌的手机,每部进货价为2500元.市场调研表明:当销售价为2900元时,平均每天能售出8部;而当销售价每降低50元时,平均每天就能多售出4部.
(1)当售价为2800元时,这种手机平均每天的销售利润达到多少元?
(2)若设每部手机降低x元,每天的销售利润为y元,试写出y与x之间的函数关系式.
(3)商场要想获得最大利润,每部手机的售价应订为为多少元?此时的最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°. 若坡角∠FAE=30°,求大树的高度. (结果保留整数,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
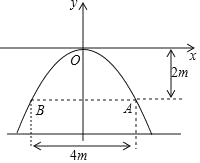
【题目】有一个截面的边缘为抛物线的拱桥桥洞,桥洞壁离水面AB的最大高度是2米,水面宽度AB为4米.把截面图形放在如图所示的平面直角坐标系中.
(1)求这条抛物线对应的函数表达式.
(2)若水面下降1米,求水面宽度增加了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017浙江省湖州市)如图,已知∠AOB=30°,在射线OA上取点O1,以O1为圆心的圆与OB相切;在射线O1A上取点O2,以O2为圆心,O2O1为半径的圆与OB相切;在射线O2A上取点O3,以O3为圆心,O3O2为半径的圆与OB相切;…;在射线O9A上取点O10,以O10为圆心,O10O9为半径的圆与OB相切.若⊙O1的半径为1,则⊙O10的半径长是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的是( )

A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
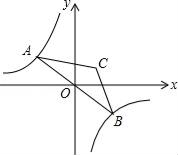
【题目】如图,点A是双曲线y=﹣![]() 在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=
在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=![]() 上运动,则k的值为_____.
上运动,则k的值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com