
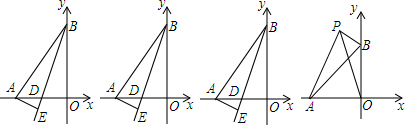
分析 (1)延长AE交BO于点F,由题意得出OA=OB,证出∠AFO=∠BDO,由AAS证明△FAO≌△DBO,得出AF=BD.证出AB=FB,由等腰三角形的三线合一性质得出AE=FE=$\frac{1}{2}$AF,即可得出结论;
(2)由直角三角形斜边上的中线性质得出OE=$\frac{1}{2}$AF=AE即可.
(3)取AB中点M,以为圆心,AM长为半径作圆,那么ABO三点皆在⊙M上;证出∠OEB=∠OAB,得出点E在⊙M上,由圆周角定理得出∠AEB=90°,即可得出结论;
(4)由∠APO=∠OBA,得出点P也在⊙M上,由圆周角定理得出∠APB=90°,即可得出结论.
解答 (1)证明:延长AE交BO于点F,如图1所示: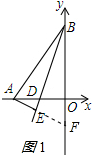
∵A(-4,0),B(0,4),
∴OA=OB,
∵AE⊥BE,
∴∠AFO+∠OBD=90°,
∵∠BDO+∠OBD=90°,
∴∠AFO=∠BDO,
在△FAO和△DBO中,
$\left\{\begin{array}{l}{∠AFO=∠BDO}&{\;}\\{∠AOF=∠BOD=90°}&{\;}\\{OA=OB}&{\;}\end{array}\right.$,
∴△FAO≌△DBO(AAS),
∴AF=BD.
在△ABF中,∵AE⊥BE,BE是∠BAF的角平分线,
∴AB=FB,
∴AE=FE=$\frac{1}{2}$AF,
∴BD=2AE;
(2)证明:在RT△AOF中,E是斜边AF的中点,
∴OE=$\frac{1}{2}$AF=AE.
(3)证明:取AB中点M,以为圆心,AM长为半径作圆,如图2所示:
则A、B、O三点皆在⊙M上;
∵OA=OB,∠AOB=90°,
∴△AOB是等腰直角三角形,
∴∠OAB=∠OBA=45°,
∴∠OEB=∠OAB,
∴点E在⊙M上,
∵AB是直径,
∴∠AEB=90°,
∴AE⊥BE;
(4)解:∵∠APO=45°,∠APO是劣弧ABO所对的圆周角,且∠APO=∠OBA,
∴点P也在⊙M上,
∵AB是直径,
∴∠APB=90°,
∴AP⊥PB.
点评 本题考查了全等三角形的判定与性质、等腰直角三角形的判定与性质、等腰三角形的性质、圆周角定理等知识;本题综合性强,有一定难度.


 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:选择题
 如图,抛物线y=-$\frac{1}{2}$x2+$\frac{7}{2}$x与矩形OABC的边AB交于点D、B,A(0,3),C(6,0),则图中抛物线与矩形OABC形成的阴影部分的面积的和为( )
如图,抛物线y=-$\frac{1}{2}$x2+$\frac{7}{2}$x与矩形OABC的边AB交于点D、B,A(0,3),C(6,0),则图中抛物线与矩形OABC形成的阴影部分的面积的和为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
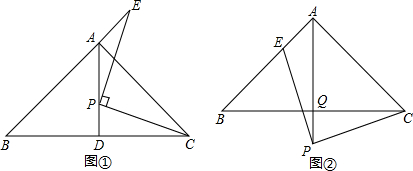
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
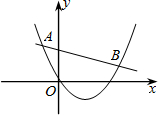 如图所示,已知二次函数y1=ax2+bx+c(a≠0)与一次函数y2=kx+m(k≠0)的图象相交于点A(-2,4),B(8,2).根据图象回答:
如图所示,已知二次函数y1=ax2+bx+c(a≠0)与一次函数y2=kx+m(k≠0)的图象相交于点A(-2,4),B(8,2).根据图象回答:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
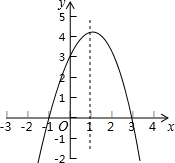 如图,在直角坐标系中,抛物线y=ax2+2x+c过点A、B且与y轴交与点C(0,3),点P为抛物线对称轴x=l上一动点.
如图,在直角坐标系中,抛物线y=ax2+2x+c过点A、B且与y轴交与点C(0,3),点P为抛物线对称轴x=l上一动点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com