
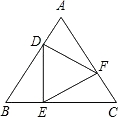
如图,等边△DEF的顶点分别在等边△ABC各边上,且DE⊥BC于E,若AB=1,则DB=__________.
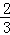 .
.
【考点】等边三角形的性质;全等三角形的判定与性质;勾股定理.
【分析】由题可证△BED≌△ADF≌△CFE,则AD=BE,由勾股定理得,BE=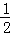 BD,因为AB=BD+AD=BD+BE=BD+
BD,因为AB=BD+AD=BD+BE=BD+ =1,所以BD=
=1,所以BD=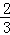 .
.
【解答】解:∵∠DEB=90°
∴∠BDE=90°﹣60°=30°
∴∠ADF=180﹣30°﹣60°=90°
同理∠EFC=90°
又∵∠A=∠B=∠C,DE=DF=EF
∴△BED≌△ADF≌△CFE
∴AD=BE,
由勾股定理得:
∵BE=
∵AB=BD+AD=BD+BE=BD+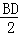 =1
=1
∴BD=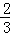 .
.
【点评】本题利用了:(1)等边三角形的性质,(2)勾股定理,(3)全等三角形 的判定和性质.
的判定和性质.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案科目:初中数学 来源: 题型:
如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等三角形的对数是( )
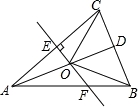
A.1对 B.2对 C.3对 D.4对
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,由四个小正方形组成的田字格中,△ABC的顶点都是小正方形的顶点.在田字格上画与△ABC成轴对称的三角形,且顶点都是小正方形的顶点,则这样的三角形(不包含△ABC本身)共有( )
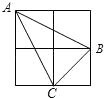
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com