
 已知:如图数轴上两点A、B所别应的分别为-3、1,点P在数轴上从点A出发以每秒钟2个单位的长度的速度向右运动,点Q在数轴上从点B出发以每秒钟1个单位长度的速度向左运动,设点P的运动时间为t秒.
已知:如图数轴上两点A、B所别应的分别为-3、1,点P在数轴上从点A出发以每秒钟2个单位的长度的速度向右运动,点Q在数轴上从点B出发以每秒钟1个单位长度的速度向左运动,设点P的运动时间为t秒.分析 (1)根据点A表示的数为-3,点B表示的数为1,根据中点坐标公式即可得到AB的中点所对应的数,进一步利用点的平移规律求得点P对应的数;
(2)可设经过x秒钟点P和点Q相遇,由路程和是AB的长,列出方程求解,进一步得出相遇点的位置即可;
(3)设点P出发y秒后,点P和点Q刚好相距1个单位长度,列出方程解答,分别求得P、Q点表示的数,设出点C表示的数,进一步利用两点之间的距离求得最小值即可.
解答 解:(1)线段AB的中点所对应的数是$\frac{-3+1}{2}$=-1,点P所对应的数是-3+2t;
(2)设经过x秒钟点P和点Q相遇,由题意得
2x+x=1-(-3)
解得:x=$\frac{4}{3}$,
点P和点Q相遇时的位置所对应的数为-3+2×$\frac{4}{3}$=-$\frac{1}{3}$;
(3)①设点P出发y秒后,点P和点Q刚好相距1个单位长度,由题意得
y12y+y=4-1,
解得:y=$\frac{2}{3}$,
点P表示为-3+$\frac{2}{3}$×2=-$\frac{5}{3}$,点Q表示为1-(1+$\frac{2}{3}$)×1=-$\frac{2}{3}$,
设此时数轴上存在-个点C,点C表示的数为a,由题意得
AC+PC+QC=|a+3|+|a+$\frac{5}{3}$|+|a+$\frac{2}{3}$|,
要使|a+3|+|a+$\frac{5}{3}$|+|a+$\frac{2}{3}$|最小,当点C与P重合时,即a=-$\frac{5}{3}$时,点C,使其到点A、点P和点Q这三点的距离和最小.
②若点P和点Q在相遇后相距1个单位长度,则2t=1×(t+1)=4+1
解得t=$\frac{4}{3}$
故P出发$\frac{4}{3}$秒后,点P和点Q也可相距1个单位长度
此时满足条件的点C即点Q,所表示的数位-$\frac{4}{3}$
综上所述,当P出发$\frac{2}{3}$秒或$\frac{4}{3}$秒时,P和Q相距1个单位长度,此时点C所表示的数分别为-$\frac{5}{3}$和-$\frac{4}{3}$
点评 此题考查一元一次方程的实际运用,利用数轴求得两点之间的距离,根据行程问题得出基本数量关系是解决问题的关键.


科目:初中数学 来源: 题型:解答题
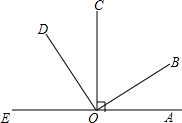 看图回答下列问题:
看图回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 销售量 | 单价 |
| 不超过100件的部分 | 2.5元/件 |
| 超过100件不超过300件的部分 | 2.2元/件 |
| 超过300件的部分 | 2元/件 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com