
【题目】如图,反比例函数y= ![]() (x>0)与一次函数y=kx+6
(x>0)与一次函数y=kx+6 ![]() 交于点C(2,4
交于点C(2,4 ![]() ),一次函数图象与两坐标轴分别交于点A和点B,动点P从点A出发,沿AB以每秒1个单位长度的速度向点B运动;同时,动点Q从点O出发,沿OA以相同的速度向点A运动,运动时间为t秒(0<t≤6),以点P为圆心,PA为半径的⊙P与AB交于点M,与OA交于点N,连接MN、MQ.
),一次函数图象与两坐标轴分别交于点A和点B,动点P从点A出发,沿AB以每秒1个单位长度的速度向点B运动;同时,动点Q从点O出发,沿OA以相同的速度向点A运动,运动时间为t秒(0<t≤6),以点P为圆心,PA为半径的⊙P与AB交于点M,与OA交于点N,连接MN、MQ.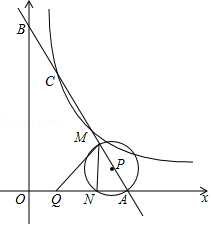
(1)求m与k的值;
(2)当t为何值时,点Q与点N重合;
(3)若△MNQ的面积为S,试求S与t的函数关系式.
【答案】
(1)
解:将C(2,4 ![]() )代入y=
)代入y= ![]() 中得,m=8
中得,m=8 ![]()
将(2,3 ![]() )代入y=kx+6
)代入y=kx+6 ![]() 中得,2k+6
中得,2k+6 ![]() =4
=4 ![]()
∴k=﹣ ![]()
(2)
解:由(1)知,k=﹣ ![]() ,
,
∴直线AB的解析式为y=﹣ ![]() x+6
x+6 ![]() ,
,
∴A(6,0),B(0,6 ![]() ),
),
∴AB=12
∵AM是直径
∴∠ANM=90°,
∴∠ANM=∠AOB
又∵∠MAN=∠BAO,
∴△MAN∽△BAO,
∴ ![]()
∵OQ=AP=t,AM=2AP=2t,OA=6,OB=6 ![]() ,AB=12
,AB=12
∴ ![]()
∴AN=t,MN= ![]() t
t
∴ON=OA﹣AN=6﹣t
∵点Q与点N重合
∴ON=OQ
即6﹣t=t
∴t=3
(3)
解:①当0<t≤3时,QN=OA﹣OQ﹣AN=6﹣2t
∴S= ![]() QNMN=
QNMN= ![]() (6﹣2t)
(6﹣2t) ![]() t=﹣
t=﹣ ![]() t2+3
t2+3 ![]() t
t
②当3<t≤6时,QN=OQ+NA﹣OA=t+t﹣6=2t﹣6
∴S= ![]() QNMN=
QNMN= ![]() (2t﹣6)
(2t﹣6) ![]() t=
t= ![]() t2﹣3
t2﹣3 ![]() t,
t,
即:S= ![]()
【解析】(1)利用待定系数法直接求出m和k;(2)先求出AB,进而判断出△MAN∽△BAO,利用比例式得出AN和MN,即可得出ON,利用ON=OQ建立方程求解即可;(3)分两种情况利用三角形的面积公式即可得出结论.
【考点精析】掌握确定一次函数的表达式和相似三角形的判定是解答本题的根本,需要知道确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS).


科目:初中数学 来源: 题型:
【题目】如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E, 
(1)求证:DE=DB;
(2)若∠BAC=90°,BD=4,求△ABC外接圆的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一组数:1,1,2,3,5,8,13,…,其中从第三个数起,每一个数都等于它前面两个数的和.现以这组数中的各个数作为正方形的长度构造一组正方形(如下图),再分别依次从左到右取2个,3个,4个,5个正方形拼成如下长方形并记为①,②,③,④,相应长方形的周长如下表所示:
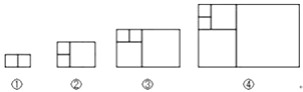

若按此规律继续作长方形,则序号为⑧的长方形周长是( )
A. 288 B. 178 C. 28 D. 110
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:①∠EBG=45°;②AG+DF=FG;③△DEF∽△ABG;④S△ABG= ![]() S△FGH . 其中正确的是( )
S△FGH . 其中正确的是( ) 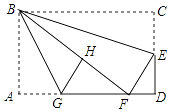
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下列各题:
(1)如图,已知直线AB与⊙O相切于点C,且AC=BC,求证:OA=OB. 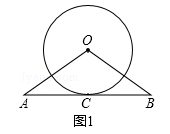
(2)如图,矩形ABCD的两条对角线相交于点O,∠AOD=120°,AB=3,求AC的长. 
查看答案和解析>>
科目:初中数学 来源: 题型:
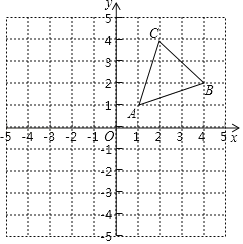
【题目】已知,在如图所示的网格中建立平面直角坐标系后,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(2,4).
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)①借助图中的网格,请只用直尺(不含刻度)在图中找一点P,使得P到AB、AC的距离相等,且PA=PB.
②若x轴上有一动点Q,使得△QAB的周长最小,则△QAB的最小周长为 .
(友情提醒:请别忘了标注宇母)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知OA⊥OB,∠AOD=∠BOC由此判定OC⊥OD,下面是推理过程,请填空.

解:∵OA⊥OB(已知)
所以_____=90°(________)
因为_____=∠AOD-∠AOC,____=∠BOC-∠AOC,∠AOD=∠BOC,
所以______=_____(等量代换)
所以______=90°
所以OC⊥OD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是矩形ABCD的对角线,过AC的中点O作EF⊥AC,交BC于点E,交AD于点F,连接AE,CF. 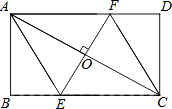
(1)求证:四边形AECF是菱形;
(2)若AB= ![]() ,∠DCF=30°,求四边形AECF的面积.(结果保留根号)
,∠DCF=30°,求四边形AECF的面积.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果市场将120吨水果运往各地商家,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨/辆) | 5 | 8 | 10 |
汽车运费(元/辆) | 400 | 500 | 600 |
(1)若全部水果都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(2)为了节约运费,市场可以调用甲、乙、丙三种车型参与运送(每种车型至少1辆),已知它们的总辆数为16辆,你能通过列方程组的方法分别求出几种车型的辆数吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com