【题目】阅读材料：
在一个三角形中，各边和它所对角的正弦的比相等， = = ，利用上述结论可以求解如下题目：
在△ABC中，∠A、∠B、∠C的对边分别为a，b，c．若∠A=45°，∠B=30°，a=6，求b．
解：在△ABC中，∵ = ∴b= = = =3 ．
理解应用：
如图，甲船以每小时30 海里的速度向正北方向航行，当甲船位于A1处时，乙船位于甲船的北偏西105°方向的B1处，且乙船从B1处按北偏东15°方向匀速直线航行，当甲船航行20分钟到达A2时，乙船航行到甲船的北偏西120°方向的B2处，此时两船相距10 海里．

（1）判断△A1A2B2的形状，并给出证明；
（2）求乙船每小时航行多少海里？

参考答案：

【答案】
（1）解：△A1A2B2是等边三角形，理由如下：

连结A1B2．

∵甲船以每小时30 海里的速度向正北方向航行，航行20分钟到达A2，

∴A1A2=30 × =10 ，

又∵A2B2=10 ，∠A1A2B2=60°，

∴△A1A2B2是等边三角形


（2）解：过点B作B1N∥A1A2，如图，

∵B1N∥A1A2，

∴∠A1B1N=180°﹣∠B1A1A2=180°﹣105°=75°，

∴∠A1B1B2=75°﹣15°=60°．

∵△A1A2B2是等边三角形，

∴∠A2A1B2=60°，A1B2=A1A2=10 ，

∴∠B1A1B2=105°﹣60°=45°．

在△B1A1B2中，

∵A1B2=10 ，∠B1A1B2=45°，∠A1B1B2=60°，

由阅读材料可知， = ，

解得B1B2= = ，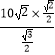

所以乙船每小时航行： ÷ =20 海里．


【解析】（1）求出A1A2=10， 已知A2B=10，可求∠A1A2B2=60度，所以△A1A2B2是等边三角形；（2）求乙船的速度须求B1B2，在△B1A1B2中可利用正弦定理，求出B1B2，再除以时间，即得速度.
【考点精析】本题主要考查了关于方向角问题的相关知识点，需要掌握指北或指南方向线与目标方向 线所成的小于90°的水平角，叫做方向角才能正确解答此题．

关闭