
【题目】如图,BC是⊙O的直径,点A在⊙O上,AD⊥BC,垂足为D,![]() =
=![]() ,BE分别交AD、AC延长线于点F、G.
,BE分别交AD、AC延长线于点F、G.
(1)过点A作直线MN,使得MN∥BG,判断直线MN与⊙O的位置关系,并说理.
(2)若AC=3,AB=4,求BG的长.
(3)连接CE,探索线段BD、CD与CE之间的数量关系,并说明理由.

【答案】(1)直线MN与⊙O相切,理由见解析;(2)BG=![]() ;(3)BD=CE+CD,理由见解析
;(3)BD=CE+CD,理由见解析
【解析】
(1)根据平行线的性质得到∠NAG=∠G,根据圆周角定理得出∠ABG=∠AEB,再由∠ABC+∠EBC=∠G+∠EAG得出∠ABC=∠G,进而得到∠NAG=∠ABC,由AB是直径得出∠BAC=90°,等量代换∠OAN=90°,求得OA⊥MN,即可得到结论;
(2)连接AE,根据圆周角定理得到∠AEB=∠ACB,根据等腰三角形的性质得到∠ABE=∠AEB,根据相似三角形的性质即可得到结论;
(3)连接CE,在BC上截取BH=CE,连接AH,根据全等三角形的判定方法得出△ABH≌△AEC(SAS),再根据全等三角形的性质即可得到结论.
解:(1)直线MN与⊙O相切,
理由:连接OA、AE

∵MN∥BG,
∴∠NAG=∠G,
∵![]() =
=![]() ,
,
∴AB=AE,∠ABG=∠AEB
∵∠EBC=∠EAC
∴∠ABC+∠EBC=∠G+∠EAG
∴∠ABC=∠G
∴∠NAG =∠ABC,
∵OA=OB
∴∠ABC=∠BAO=∠NAG
∵AB是直径
∴∠BAC=90°即∠BAO+∠OAC=90°
∴∠NAG+∠OAC=90°
即∠NAO=90°
∴OA⊥MN,
∴直线MN与⊙O相切;
(2)解:连接AE,
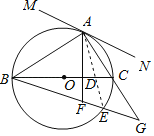
由(1)可知:∠ABC=∠G
∵∠BAC=∠GAB,
∴△ABC∽△AGB,
∴![]() ,
,
∵BC是⊙O的直径,
∴∠BAC=90°,
∵AC=3,AB=4,
∴BC=5,
∴![]() ,
,
∴BG=![]() ;
;
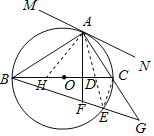
(3)解:BD=CE+CD,
理由:连接CE,
在BC上截取BH=CE,连接AH,
∵AB=AE,
又∵∠ABC=∠AEC,
∴△ABH≌△AEC(SAS),
∴AH=AC,
又∵AD⊥BC,
∴HD=CD,
∴BD=BH+HD=CE+CD.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E是BC的中点,且∠AEC=∠DCE,则下列结论不正确的是( )
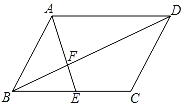
A.S△AFD=2S△EFBB.BF=![]() DF
DF
C.AE=DCD.∠AEB=∠ADC
查看答案和解析>>
科目:初中数学 来源: 题型:
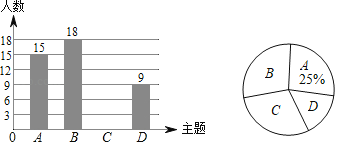
【题目】为了响应市政府号召,某校开展了“四城同创,共建美好家园”活动周,活动周设置了“A:文明礼仪,B:生态环境,C:交通安全,D:卫生保洁”四个主题,每个学生选一个主题参与.为了解活动开展情况,学校随机抽取了部分学生进行调查,并根据调查结果绘制了如下条形统计图和扇形统计图.
(1)本次随机调查的学生人数是 人;
(2)在扇形统计图中,“C”所在扇形的圆心角等于 度;
(3)如果该校共有学生2400人,请你估计参与“文明礼仪”主题的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地.两人之间的距离y(米)与时间t(分钟)之间的函数关系如图所示.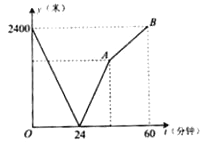
(1)根据图象信息,当t=________分钟时甲乙两人相遇,甲的速度为________米/分钟;
(2)求出线段AB所表示的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(﹣3,y1),B(2,y2)均在抛物线y=ax2+bx+c上,点P(m,n)是该抛物线的顶点,若y1>y2≥n,则m的取值范围是( )
A.﹣3<m<2B.﹣![]() <m<-
<m<-![]() C.m>﹣
C.m>﹣![]() D.m>2
D.m>2
查看答案和解析>>
科目:初中数学 来源: 题型:
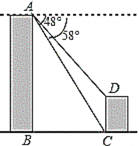
【题目】如图,甲、乙两座建筑物的水平距离![]() 为
为![]() ,从甲的顶部
,从甲的顶部![]() 处测得乙的顶部
处测得乙的顶部![]() 处的俯角为48°,测得底部
处的俯角为48°,测得底部![]() 处的俯角为53°,求甲、乙建筑物的高度
处的俯角为53°,求甲、乙建筑物的高度![]() 和
和![]() (结果用含非特珠角的三角函数表示即可).
(结果用含非特珠角的三角函数表示即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】文具店有三种品牌的6个笔记本,价格是4,5,7(单位:元)三种,从中随机拿出一个本,已知![]() (一次拿到7元本)
(一次拿到7元本)![]() .
.
(1)求这6个本价格的众数.
(2)若琪琪已拿走一个7元本,嘉嘉准备从剩余5个本中随机拿一个本.
①所剩的5个本价格的中位数与原来6个本价格的中位数是否相同?并简要说明理由;
②嘉嘉先随机拿出一个本后不放回,之后又随机从剩余的本中拿一个本,用列表法求嘉嘉两次都拿到7元本的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了调查某小区居民的用水情况,随机抽查了若干个家庭的![]() 月份用水量,结果如下表:
月份用水量,结果如下表:
月用水量(立方米) |
|
|
|
|
户数 |
|
|
|
|
根据上表解决下列问题:
(1)这组数据的众数是 ,中位数是 ;
(2)求这若干个家庭的![]() 月份平均用水量;
月份平均用水量;
(3)请根据(2)的结论估计该小区![]() 个家庭
个家庭![]() 月份总用水量.
月份总用水量.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com